
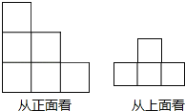
【题目】用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,某大楼的顶部竖有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() ,
, ![]() )
)
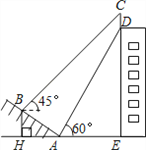
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织初二年级400名学生到威海参加拓展训练活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金250元,大客车每辆租金350元,请选出最省线的租车方案,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
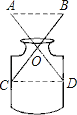
【题目】小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸在里边直接测,于是她想了想,唉!有办法了.她拿来了两根长度相同的细木条,并且把两根长木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道这是为什么吗?请说明理由.(木条的厚度不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
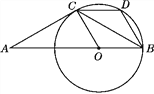
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州市在今年三月份启动实施“明眸皓齿”工程.根据安排,某校对于学生使用电子产品的一周用时情况进行抽样调查,绘制成以下频数分布直方图.请根据图中提供的信息,解答下列问题.

(1)这次共抽取了 名学生进行调查.
(2)用时在2.45~3.45小时这组的频数是_ , 频率是_ .
(3)如果该校有1000名学生,请估计一周电子产品用时在0.45~3.45小时的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com