
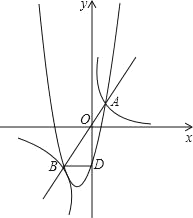
【题目】如图,直角坐标系中y=mx和![]() (m>0)图象的交点为A、B,BD⊥y轴于D,S△ABD=4;直线A′B′由直线AB缓慢向下平移;
(m>0)图象的交点为A、B,BD⊥y轴于D,S△ABD=4;直线A′B′由直线AB缓慢向下平移;
(1)求m的值;
(2)问直线A′B′向下平移多少单位时与经过B、D、A三点的抛物线刚好只有一个交点,并求出交点坐标.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:不相交的两个函数图象在竖直方向上的最短距离为这两个函数的“亲近距离”
(1)求抛物线y=x2﹣2x+3与x轴的“亲近距离”;
(2)在探究问题:求抛物线y=x2﹣2x+3与直线y=x﹣1的“亲近距离”的过程中,有人提出:过抛物线的顶点向x轴作垂线与直线相交,则该问题的“亲近距离”一定是抛物线顶点与交点之间的距离,你同意他的看法吗?请说明理由.
(3)若抛物线y=x2﹣2x+3与抛物线y=![]() +c的“亲近距离”为
+c的“亲近距离”为![]() ,求c的值.
,求c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
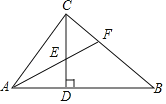
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚筒轮⊙A,⊙A与水平地面相切于点D,在拉杆伸长到最大的情况下,当点B距离水平地面34cm时,点C到水平地面的距离CE为55cm.设AF∥ MN.

(1)求⊙A的半径.
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果精确到1cm,参考数据:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,弦
中,弦![]() 垂直于直径
垂直于直径![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,将
,将![]() 沿
沿![]() 翻转得到
翻转得到![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
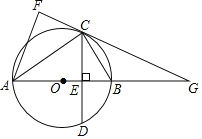
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,①求证:四边形
的中点,①求证:四边形![]() 是菱形;②若
是菱形;②若![]() ,求
,求![]() 的半径长.
的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
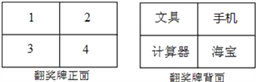
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格上有6个斜三角形:
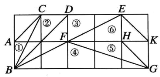
①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
在②~⑥中,与①相似的三角形的序号是____.(把你认为正确的都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )
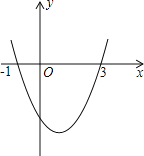
A.3个B.2个C.1个D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com