
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþl1£Ωk1x+b”Î∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛΩª”⁄A£¨B¡Ωµ„£®µ„A‘⁄µ„B◊Û≤ý£©£¨“—÷™µ„Aµƒ◊¯±Í «£®6£¨2£©µ„Bµƒ◊ð◊¯±Í «©Å3£Æ
µƒÕºœÛΩª”⁄A£¨B¡Ωµ„£®µ„A‘⁄µ„B◊Û≤ý£©£¨“—÷™µ„Aµƒ◊¯±Í «£®6£¨2£©µ„Bµƒ◊ð◊¯±Í «©Å3£Æ
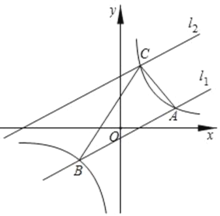
£®1£©«Û∑¥±»¿˝∫Ø ˝∫Õ÷±œþl1µƒ±Ì¥Ô Ω£ª
£®2£©∏˘æðÕºœÛ÷±Ω”–¥≥ˆk1x+b£æ![]() µƒΩ‚ºØ£ª
µƒΩ‚ºØ£ª
£®3£©Ω´÷±œþl1£∫![]() —ÿy÷·œÚ…œ∆Ω“∆∫Ûµƒ÷±œþl2”Î∑¥±»¿˝∫Ø ˝
—ÿy÷·œÚ…œ∆Ω“∆∫Ûµƒ÷±œþl2”Î∑¥±»¿˝∫Ø ˝![]() ‘⁄µ⁄“ªœÛœÞƒ⁄Ωª”⁄µ„C£¨»Áπ˚°˜ABCµƒ√ʪ˝Œ™30£¨«Û∆Ω“∆∫Ûµƒ÷±œþl2µƒ∫Ø ˝±Ì¥Ô Ω£Æ
‘⁄µ⁄“ªœÛœÞƒ⁄Ωª”⁄µ„C£¨»Áπ˚°˜ABCµƒ√ʪ˝Œ™30£¨«Û∆Ω“∆∫Ûµƒ÷±œþl2µƒ∫Ø ˝±Ì¥Ô Ω£Æ
°æ¥∞∏°ø£®1£©y£Ω![]() £¨y£Ω
£¨y£Ω![]() x©Å1£ª£®2£©©Å4£ºx£º0ªÚx£æ6£ª£®3£©y£Ω
x©Å1£ª£®2£©©Å4£ºx£º0ªÚx£æ6£ª£®3£©y£Ω![]() x+5£Æ
x+5£Æ
°æΩ‚Œˆ°ø
£®1£©Ω´µ„A£®6£¨2£©¥˙»Î![]() £¨«Û≥ˆk2£Ω12£¨µ√µΩ∑¥±»¿˝∫Ø ˝µƒ±Ì¥Ô Ω£ªΩ´y£Ω3¥˙»Î£¨«Û≥ˆx£¨µ√µΩBµ„◊¯±Í£¨‘ŸΩ´A£¨B¡Ωµ„µƒ◊¯±Í¥˙»Îl1£Ωk1x£´b£¨¿˚”√¥˝∂®œµ ˝∑®«Û≥ˆ÷±œþl1µƒ±Ì¥Ô Ω£ª
£¨«Û≥ˆk2£Ω12£¨µ√µΩ∑¥±»¿˝∫Ø ˝µƒ±Ì¥Ô Ω£ªΩ´y£Ω3¥˙»Î£¨«Û≥ˆx£¨µ√µΩBµ„◊¯±Í£¨‘ŸΩ´A£¨B¡Ωµ„µƒ◊¯±Í¥˙»Îl1£Ωk1x£´b£¨¿˚”√¥˝∂®œµ ˝∑®«Û≥ˆ÷±œþl1µƒ±Ì¥Ô Ω£ª
£®2£©’“≥ˆ“ª¥Œ∫Ø ˝¬‰‘⁄∑¥±»¿˝∫Ø ˝ÕºœÛ…œ∑Ωµƒ≤ø∑÷∂‘”¶µƒ◊‘±‰¡øxµƒ»°÷µ∑∂Œßº¥ø…£ª
£®3£©…Ë÷±œþl1”Îx÷·Ωª”⁄µ„E£¨∆Ω“∆∫Ûµƒ÷±œþl2”Îx÷·Ωª”⁄µ„D£¨¡¨Ω”AD£¨BD£¨“¿æðCD°ŒAB£¨º¥ø…µ√≥ˆ°˜ABCµƒ√ʪ˝”ΰ˜ABDµƒ√ʪ˝œýµ»£¨«Ûµ√D£®10£¨0£©£¨º¥ø…µ√≥ˆ∆Ω“∆∫Ûµƒ÷±œþl2µƒ∫Ø ˝±Ì¥Ô Ω£Æ
£®1£©°þ∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛπ˝µ„A£®6£¨2£©£¨
µƒÕºœÛπ˝µ„A£®6£¨2£©£¨
°ýk2£Ω6°¡2£Ω12£¨
°ý∑¥±»¿˝∫Ø ˝µƒ±Ì¥Ô ΩŒ™y£Ω![]() £¨
£¨
°þ∑¥±»¿˝∫Ø ˝y£Ω![]() µƒÕºœÛπ˝µ„B£¨Bµƒ◊ð◊¯±Í «©Å3£¨
µƒÕºœÛπ˝µ„B£¨Bµƒ◊ð◊¯±Í «©Å3£¨
°ýy£Ω©Å3 ±£¨x£Ω©Å4£¨
°ýB£®©Å4£¨©Å3£©£Æ
°þ÷±œþl1£Ωk1x+bπ˝A£¨B¡Ωµ„£¨
°ý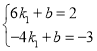 £¨Ω‚µ√
£¨Ω‚µ√ £¨
£¨
°ý÷±œþl1µƒ±Ì¥Ô ΩŒ™y£Ω![]() x©Å1£ª
x©Å1£ª
£®2£©∏˘æðÕºœÛ£¨ø…÷™µ±©Å4£ºx£º0ªÚx£æ6 ±£¨“ª¥Œ∫Ø ˝µƒÕºœÛ‘⁄∑¥±»¿˝∫Ø ˝ÕºœÛµƒ…œ∑Ω£¨
À˘“‘k1x+b£æ![]() µƒΩ‚ºØŒ™©Å4£ºx£º0ªÚx£æ6£ª
µƒΩ‚ºØŒ™©Å4£ºx£º0ªÚx£æ6£ª
£®3£©»ÁÕº£¨…Ë÷±œþl1”Îx÷·Ωª”⁄µ„E£¨∆Ω“∆∫Ûµƒ÷±œþl2”Îx÷·Ωª”⁄µ„D£¨¡¨Ω”AD£¨BD£¨
°þCD°ŒAB£¨
°ý°˜ABCµƒ√ʪ˝”ΰ˜ABDµƒ√ʪ˝œýµ»£¨
°þ°˜ABCµƒ√ʪ˝Œ™30£¨
°ýS°˜ADE+S°˜BDE£Ω30£¨º¥![]() DE£®|yA|+|yB|£©£Ω30£¨
DE£®|yA|+|yB|£©£Ω30£¨
°ý![]() °¡DE°¡5£Ω30£¨
°¡DE°¡5£Ω30£¨
°ýOD£Ω12£¨
°þE£®
°ýD£®©Å10£¨0£©£¨
…Ë∆Ω“∆∫Ûµƒ÷±œþl2µƒ∫Ø ˝±Ì¥Ô ΩŒ™y£Ω![]() x+n£¨
x+n£¨
∞—D£®©Å10£¨0£©¥˙»Î£¨ø…µ√0£Ω![]() °¡£®©Å10£©+n£¨
°¡£®©Å10£©+n£¨
Ω‚µ√n£Ω5£¨
°ý∆Ω“∆∫Ûµƒ÷±œþl2µƒ∫Ø ˝±Ì¥Ô ΩŒ™y£Ω![]() x+5£Æ
x+5£Æ




| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ƒ≥–£Ω×߬•ABµƒ∫Û√Ê”–“ªΩ®÷˛ŒÔCD£¨µ±π‚œþ”εÿ√ʵƒº–Ω« «22 ±£¨
Ω×߬•‘⁄Ω®÷˛ŒÔµƒ«Ω…œ¡Ùœ¬∏þ2mµƒ”∞◊”CE£ª∂¯µ±π‚œþ”εÿ√ʵƒº–Ω« «45 ±£¨Ω×߬•∂•A‘⁄µÿ√Ê…œµƒ”∞◊”F”ΫΩΩ«C”–13mµƒæý¿Î(B°¢F°¢C‘⁄“ªÃı÷±œþ…œ)£Æ
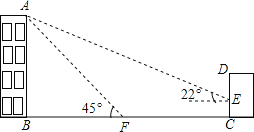
(1)«ÛΩ×߬•ABµƒ∏þ∂»£ª
(2)—ß–£“™‘⁄A°¢E÷ƺ‰π““ª–©≤ ∆Ï£¨«Îƒ„«Û≥ˆA°¢E÷ƺ‰µƒæý¿Î(Ω·π˚±£¡Ù’˚ ˝)£Æ
(≤Œøº ˝æð£∫sin22°÷![]() £¨cos22°÷
£¨cos22°÷![]() £¨tan22°÷
£¨tan22°÷![]() )
)
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
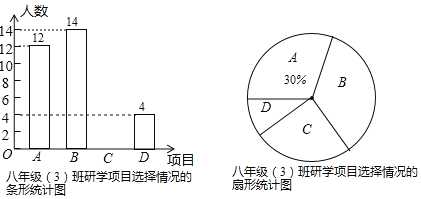
°æƒø°øƒ≥—ß–£ø™’π“‘Àÿ÷ ÷…˝Œ™÷˜Ã‚µƒ—–—ߪÓ∂Ø£¨Õ∆≥ˆ¡À“‘œ¬Àƒ∏ˆœÓƒøπ©—ß…˙—°‘Ò£∫A£Æƒ£ƒ‚ºð ª£ªB£Ææ¸ ¬æ∫ºº£ªC£Æº“œÁµº”Œ£ªD£Æ÷≤ŒÔ ∂±£Æ—ß–£πÊ∂®£∫√ø∏ˆ—ß…˙∂º±ÿ–α®√˚«“÷ªƒÐ—°‘Ò∆‰÷–“ª∏ˆœÓƒø£Æ∞ÀƒÍº∂£®3£©∞ý∞ý÷˜»Œ¡ı¿œ ¶∂‘»´∞ý—ß…˙—°‘ÒµƒœÓƒø«ÈøˆΩ¯––¡ÀÕ≥º∆£¨≤¢ªÊ÷∆¡À»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ«ÎΩ·∫œÕ≥º∆Õº÷–µƒ–≈œ¢£¨Ω‚戜¬¡–Œ £∫
£®1£©∞ÀƒÍº∂£®3£©∞ý—ß…˙◊лÀ ˝ «°° °°£¨≤¢Ω´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®2£©¡ı¿œ ¶∑¢œ÷±®√˚≤Œº”°∞÷≤ŒÔ ∂±°±µƒ—ß…˙÷–«°∫√”–¡Ω√˚ƒ–…˙£¨œ÷◊º±∏¥”’‚–©—ß…˙÷–»Œ“‚ÃÙ—°¡Ω√˚µ£»ŒªÓ∂غ«¬º‘±£¨«Î”√¡–±ÌªÚª≠ ˜◊¥Õºµƒ∑Ω∑®£¨«Û«°∫√—°÷–1√˚ƒ–…˙∫Õ1√˚≈Æ…˙µ£»ŒªÓ∂غ«¬º‘±µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
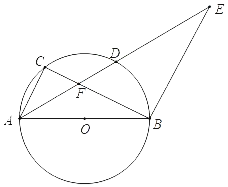
°æƒø°ø»ÁÕº£¨AB «°—Oµƒ÷±æ∂£¨µ„C «‘≤…œ“ªµ„£¨µ„D «![]() µƒ÷–µ„£¨—”≥§AD÷¡µ„E£¨ πµ√AB£ΩBE£Æ
µƒ÷–µ„£¨—”≥§AD÷¡µ„E£¨ πµ√AB£ΩBE£Æ
£®1£©«Û÷§£∫°˜ACF°◊°˜EBF£ª
£®2£©»ÙBE£Ω10£¨tanE£Ω![]() £¨«ÛCFµƒ≥§£Æ
£¨«ÛCFµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨CB£ΩCA£¨°œACB£Ω90°„£¨µ„D‘⁄±þBC…œ(”ÎB£¨C≤ª÷ÿ∫œ)£¨Àƒ±þ–ŒADEFŒ™’˝∑Ω–Œ£¨π˝µ„F◊˜FG°ÕCA£¨ΩªCAµƒ—”≥§œþ”⁄µ„G£¨¡¨Ω”FB£¨ΩªDE”⁄µ„Q£¨∏¯≥ˆ“‘œ¬Ω·¬€£∫¢ŸAC£ΩFG£ª¢⁄S°˜FAB°√SÀƒ±þ–ŒCBFG£Ω1°√2£ª¢€°œABC£Ω°œABF£ª¢ÐAD2£ΩFQ°§AC£¨∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝ «(°°°°)
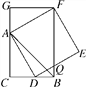
A. 1∏ˆ B. 2∏ˆ C. 3∏ˆ D. 4∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
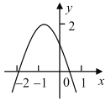
°æƒø°ø»ÁÕºÀ˘ 棨∂˛¥Œ∫Ø ˝![]() µƒÕºœÛ£¨«“”Î
µƒÕºœÛ£¨«“”Î![]() ÷·Ωªµ„µƒ∫·◊¯±Í∑÷±Œ™
÷·Ωªµ„µƒ∫·◊¯±Í∑÷±Œ™![]() £¨
£¨![]() £¨∆‰÷–
£¨∆‰÷–![]() £¨
£¨![]() £¨œ¬¡–Ω·¬€£∫¢Ÿ
£¨œ¬¡–Ω·¬€£∫¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]() .’˝»∑µƒÀµ∑®”–£∫______.£®«Î–¥À˘”–’˝»∑Àµ∑®µƒ–Ú∫≈£©
.’˝»∑µƒÀµ∑®”–£∫______.£®«Î–¥À˘”–’˝»∑Àµ∑®µƒ–Ú∫≈£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Ãð–Œ![]() ÷–£¨
÷–£¨![]() °Œ
°Œ![]() £¨«“
£¨«“![]() £¨
£¨![]() £¨
£¨![]() °£
°£
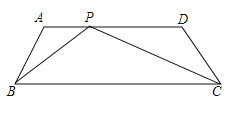
¢≈»ÁÕº£¨PŒ™![]() …œµƒ“ªµ„£¨¬˙◊„°œBPC=°œA£¨«ÛAPµƒ≥§£ª
…œµƒ“ªµ„£¨¬˙◊„°œBPC=°œA£¨«ÛAPµƒ≥§£ª
¢∆»Áπ˚µ„P‘⁄![]() ±þ…œ“∆∂Ø£®µ„P”ε„
±þ…œ“∆∂Ø£®µ„P”ε„![]() ≤ª÷ÿ∫œ£©£¨«“¬˙◊„°œBPE=°œA£¨
≤ª÷ÿ∫œ£©£¨«“¬˙◊„°œBPE=°œA£¨![]() Ωª÷±œþ
Ωª÷±œþ![]() ”⁄µ„E£¨Õ¨ ±Ωª÷±œþDC”⁄µ„
”⁄µ„E£¨Õ¨ ±Ωª÷±œþDC”⁄µ„![]() °£
°£
¢Ÿµ±µ„![]() ‘⁄œþ∂ŒDCµƒ—”≥§œþ…œ ±£¨…Ë
‘⁄œþ∂ŒDCµƒ—”≥§œþ…œ ±£¨…Ë![]() £¨CQ=y£¨«Û
£¨CQ=y£¨«Û![]() πÿ”⁄
πÿ”⁄![]() µƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆ◊‘±‰¡ø
µƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆ◊‘±‰¡ø![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
¢⁄–¥CE=1 ±£¨–¥≥ˆAPµƒ≥§£®≤ª±ÿ–¥Ω‚¥π˝≥ã©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
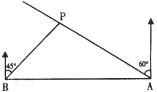
°æƒø°ø»ÁÕº£¨‘⁄“ª± ÷±µƒ∫£∞∂œþ…œ”–A£¨B¡Ω∏ˆπ€≤‚’棨A‘⁄Bµƒ’˝∂´∑ΩœÚ£¨”–“ªÀ“–°¥¨Õ£‘⁄µ„P¥¶£¨¥”A≤‚µ√–°¥¨‘⁄±±∆´Œ˜60°„µƒ∑ΩœÚ£¨¥”B≤‚µ√–°¥¨‘⁄±±∆´∂´45°„µƒ∑ΩœÚ£¨BP=6![]() km.
km.
(1)«ÛA°¢B¡Ωπ€≤‚’æ÷ƺ‰µƒæý¿Î£ª
(2)–°¥¨¥”µ„P¥¶—ÿ…‰œþAPµƒ∑ΩœÚ«∞––£¨«Ûπ€≤‚’æB”Ζ°¥¨µƒ◊Ó∂Ãæý¿Î.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…Ã∆∑µƒΩ¯º€Œ™√øº˛30‘™£¨ €º€Œ™√øº˛40‘™£¨√ø÷Ðø…¬Ù≥ˆ180º˛£ª»Áπ˚√øº˛…Ã∆∑µƒ €º€√ø…œ’«1‘™£¨‘Ú√ø÷ÐæÕª·…Ÿ¬Ù≥ˆ5º˛£¨µ´√øº˛ €º€≤ªƒÐ∏þ”⁄55‘™£¨…Ë√øº˛…Ã∆∑µƒ €º€…œ’«x‘™(xŒ™’˚ ˝)£¨√ø÷еƒœ˙ €¿˚»ÛŒ™y‘™£Æ
(1)«Ûy”Îxµƒ∫Ø ˝πÿœµ Ω£¨≤¢÷±Ω”–¥≥ˆ◊‘±‰¡øxµƒ»°÷µ∑∂Œß£ª
(2)√øº˛…Ã∆∑µƒ €º€Œ™∂ý…Ÿ‘™ ±£¨√ø÷Ðø…ªÒµ√◊Ó¥Û¿˚»Û£ø◊Ó¥Û¿˚»Û «∂ý…Ÿ£ø
(3)√øº˛…Ã∆∑µƒ €º€∂®Œ™∂ý…Ÿ‘™ ±£¨√ø÷еƒ¿˚»Û«°∫√ «2145‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com