
【题目】4月23日为世界阅读日,为响应党中央“倡导全民阅读,建设书香社会”的号召,某校团委组织了一次全校学生参加的“读书活动”大赛,为了了解本次大赛的成绩,校团委随机抽取了部分学生的成绩(成绩![]() 取整数,总分100分)作为样本进行统计,绘制了如下不完整的频数频率分布表和频数分布直方图:
取整数,总分100分)作为样本进行统计,绘制了如下不完整的频数频率分布表和频数分布直方图:
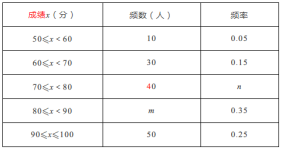
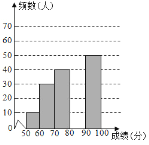
根据所给信息,解答下列问题
(1)抽取的样本容量是 .![]() .
.![]() .
.
(2)补全频数分布直方图,这200名学生成绩的中位数会落在 分数段;
(3)全校有1200名学生参加比赛,若得分为90分及以上为优秀,请你估计全校参加比赛成绩优秀的学生人数
【答案】(1)200,70,0.2;(2)见解析,70-80;(3)300人.
【解析】
(1)根据50≤x<60这一组的频数和频率,可以得到抽取样本的样本容量,然后即可得到m和n的值;
(2)根据(1)中m的值,可以将频数分布直方图补充完整,然后根据频数分布表中的数据,可以得到这200名学生成绩的中位数会落在哪一组;
(3)根据频数分布表中的数据,可以计算出全校参加比赛成绩优秀的学生人数.
解:(1)抽取的样本容量是:10÷0.05=200,
m=200×0.35=70,
n=40÷200=0.2,
故答案为:200,70,0.2;
(2)由(1)知,m=70,
补全的频数分布直方图如图所示,
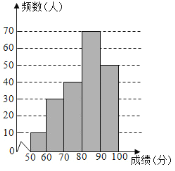
这200名学生成绩的中位数会落在80≤x<90分数段,
故答案为:80≤x<90;
(3)1200×0.25=300(人),
答:全校参加比赛成绩优秀的学生有300人.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
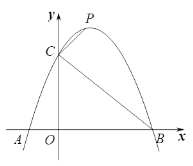
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在![]() 与
与![]() 中,
中,![]() ,且
,且![]() 所以称
所以称![]() 与
与![]() 为“关联等腰三角形”,设它们的顶角为
为“关联等腰三角形”,设它们的顶角为![]() ,连接
,连接![]() ,则称
,则称![]() 会为“关联比".
会为“关联比".
下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:
[特例感知]
![]() 当
当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,
时,
①在图1中,若点![]() 落在
落在![]() 上,则“关联比”
上,则“关联比”![]() =
=
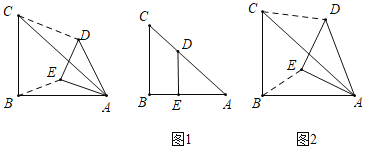
②在图2中,探究![]() 与
与![]() 的关系,并求出“关联比”
的关系,并求出“关联比”![]() 的值.
的值.

[类比探究]
![]() 如图3,
如图3,
①当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() =
=
②猜想:当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() = (直接写出结果,用含
= (直接写出结果,用含![]() 的式子表示)
的式子表示)
[迁移运用]
![]() 如图4,
如图4, ![]() 与
与![]() 为“关联等腰三角形”.若
为“关联等腰三角形”.若![]() 点
点![]() 为
为![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 为
为![]() 上一动点,求点
上一动点,求点![]() 自点
自点![]() 运动至点
运动至点![]() 时,点
时,点![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 点
点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿折线
的速度沿折线![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 运动,
运动,![]() 两点同时出发,当某一点运动到点
两点同时出发,当某一点运动到点![]() 时,两点同时停止运动设运动时间为
时,两点同时停止运动设运动时间为![]() 的面积为
的面积为![]() 关于
关于![]() 的函数图像由
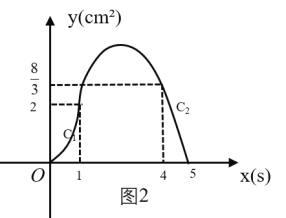
的函数图像由![]() 两段组成,如图2所示.
两段组成,如图2所示.
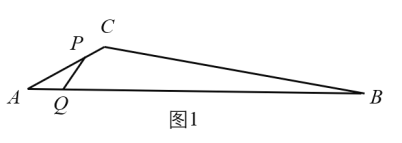
(1)求![]() 的值;
的值;
(2)求图2中图像![]() 段的函数表达式;
段的函数表达式;
(3)当点![]() 运动到线段
运动到线段![]() 上某一段时,
上某一段时,![]() 的面积大于当点
的面积大于当点![]() 在线段
在线段![]() 上任意一点时
上任意一点时![]() 的面积,求
的面积,求![]() 的取值范围.(直接写出答案)
的取值范围.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小超骑电动车、小生骑自行车分别同时从甲、乙两地出发,匀速相向而行,在![]() 分钟时两人相遇,在行驶的过程中,小超到达乙地后停留一会,再按原路原速返回甲地,小生一直匀速骑自行车
分钟时两人相遇,在行驶的过程中,小超到达乙地后停留一会,再按原路原速返回甲地,小生一直匀速骑自行车![]() 后,与小超同时到达甲地,如图表示两人距乙地的距离
后,与小超同时到达甲地,如图表示两人距乙地的距离![]() 与时间
与时间![]() 之间的函数关系.
之间的函数关系.
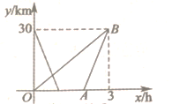
(1)小超骑车的速度_ ![]() ,小生骑车的速度
,小生骑车的速度 ![]() ;
;
(2)求线段![]() 的解析式;
的解析式;
(3)如果小超不在乙地停留,按原路原速直接返回,问在小超回到甲地之前,小超何时能追上小生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“普洱茶”是云南有名的特产,某网店专门销售某种品牌的普洱茶,成本为30元/盒,每天销售![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天该种普洱茶的销售量不低于240盒,该网店店主热心公益事业,决定从每天的销售利润中捐出500元给扶贫基金会,当销售单价为多少元时,每天获取的净利润最大,最大净利润是多少?(注:净利润=总利润-捐款)
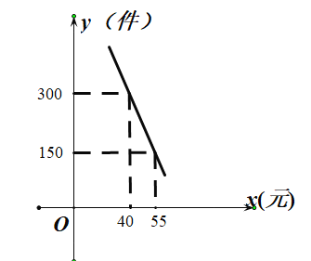
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书法是我国的文化瑰宝,研习书法能培养高雅的品格某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示,并将测试结果绘制成如下两幅不完整的统计图.
表示,并将测试结果绘制成如下两幅不完整的统计图.
书写能力等级测试条形统计图:
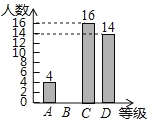
书写能力等级测试扇形统计图:
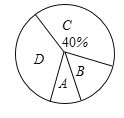
请根据统计图中的信息解答以下问题:
(1)本次抽取的学生共有______人,扇形统计图中![]() 所对应扇形的圆心角是_______
所对应扇形的圆心角是_______![]() ;
;
(2)把条形统计图补充完整;
(3)依次将优秀、良好、及格、不及格记为![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,则抽取的这部分学生书写成绩的众数是_______,中位数是_______,平均数是________;
分,则抽取的这部分学生书写成绩的众数是_______,中位数是_______,平均数是________;
(4)若该校共有学生![]() 人,请估计一下,书写能力等级达到优秀的学生大约有多少人?
人,请估计一下,书写能力等级达到优秀的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
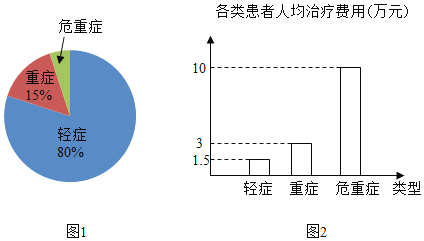
【题目】今年2﹣4月某市出现了200名新冠肺炎患者,市委根据党中央的决定,对患者进行了免费治疗.图1是该市轻症、重症、危重症三类患者的人数分布统计图(不完整),图2是这三类患者的人均治疗费用统计图.请回答下列问题.
(1)轻症患者的人数是多少?
(2)该市为治疗危重症患者共花费多少万元?
(3)所有患者的平均治疗费用是多少万元?
(4)由于部分轻症患者康复出院,为减少病房拥挤,拟对某病房中的A、B、C、D、E五位患者任选两位转入另一病房,请用树状图法或列表法求出恰好选中B、D两位患者的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一把折叠椅子,图2是椅子完全打开支稳后的侧面示意图,![]() 表示地面所在的直线,其中
表示地面所在的直线,其中![]() 和
和![]() 表示两根较粗的钢管,
表示两根较粗的钢管,![]() 表示座板平面,
表示座板平面,![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,
,![]() 长
长![]() ,
,![]() ,
,![]() ,
,![]() 长
长![]() ,
,![]() 长
长![]() ,
,
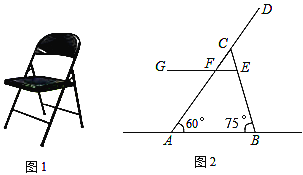
(1)求座板![]() 的长;
的长;
(2)求此时椅子的最大高度(即点![]() 到直线
到直线![]() 的距离).(结果保留根号)
的距离).(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com