
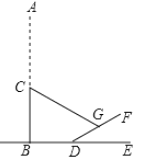
【题目】如图,一棵与地面垂直的笔直大树![]() ,在
,在![]() 点处被大风折断后,
点处被大风折断后,![]() 部分倒下,树的顶端
部分倒下,树的顶端![]() 与斜坡
与斜坡![]() 上的点
上的点![]() 重合(
重合(![]() 都保持笔直),经测量
都保持笔直),经测量![]() ,
,![]() ,则树高
,则树高![]() 为_______米(保留根号).
为_______米(保留根号).
【答案】![]()
【解析】
过点C作CM∥BE交DF的延长线于点M,过点M作MN⊥BE的延长线于点N,过点G作GH⊥CM于点H,设CG=2x,根据题意列出方程求出x的值后即可求出AB的长度.
过点C作CM∥BE交DF的延长线于点M,过点M作MN⊥BE的延长线于点N,
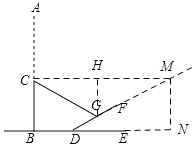
过点G作GH⊥CM于点H,
∵∠CGD=60°,∠FDE=30°,
∴∠CMG=30°,
∴∠GCM=30°,
∴CG=GM,
设CG=2x,
∴CH=![]() x,
x,
∴CM=2![]() x,
x,
∵DG=2,
∴DM=2+2x,
∴MN=1+x,DN=![]() (1+x),
(1+x),
∴BN=3+![]() (1+x),
(1+x),
∵CM=BN,
∴2![]() x=3+
x=3+![]() (1+x),
(1+x),
解得:x=![]() +1,
+1,
∴MN=BC=2+![]() ,
,
∴AB=CB+CG
=2+![]() +2
+2![]() +2
+2
=4+3![]() ,
,
故答案为:4+3![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
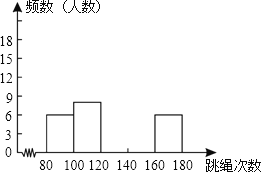
【题目】为了进一步了解某校九年级1000名学生的身体素质情况,体育老师对该校九年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,试估计该年级学生不合格的人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人跳100个以上(含100个)为优秀.下表是甲班和乙班5名学生的比赛数据(每跳1个记1分,单位:分):
1号 | 2号 | 3号 | 4号 | 5号 | 总计 | |
甲班 | 100 | 98 | 110 | 89 | m | 500 |
乙班 | 89 | n | 95 | 119 | 97 | 500 |
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,来确定冠军.请你回答下列问题:
(1)上表中,m=______,n=_____;
(2)若从两班参赛的这10名同学中,随机选择1人,求其成绩为优秀的概率;
(3)试从两班比赛成绩的优秀率、中位数和极差三个方面加以分析,判断冠军应该属于哪个班级?并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张卡片(背面完全相同)分别写有![]() ,
,![]() ,
,![]() ,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.
,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.
![]() 两人抽取的卡片上的数是
两人抽取的卡片上的数是![]() 的概率是________.
的概率是________.
![]() 李刚为他们俩设定了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小军获胜,否则小明获胜,你认为这个游戏规则对谁有利?请用列表法或树状图进行分析说明.
李刚为他们俩设定了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小军获胜,否则小明获胜,你认为这个游戏规则对谁有利?请用列表法或树状图进行分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用![]() (元)随时间
(元)随时间![]() (天)的变化图象为折线
(天)的变化图象为折线![]() ,如图所示.
,如图所示.
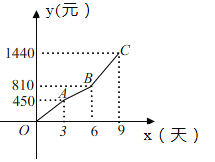
(1)当租赁时间不超过3天时,求每日租金.
(2)当![]() 时,求
时,求![]() (元)与
(元)与![]() (天)的函数关系式.
(天)的函数关系式.
(3)甲、乙两人租赁该款汽车各一辆,两人租赁的时间共为9天,甲租的天数少于3天,乙比甲多支付费用720元.请问乙租这款汽车多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营一种商品,进价是每千克30元,根据市场调查发现,每日的销售量![]() (千克)与售价
(千克)与售价![]() (元/千克)满足一次函数关系.下表记录的是某两日的有关数据:
(元/千克)满足一次函数关系.下表记录的是某两日的有关数据:
| 35 | 40 |
| 850 | 800 |
(1)求![]() 与
与![]() 的函数关系式(不求自变量的取值范围);
的函数关系式(不求自变量的取值范围);
(2)在销售过程中销售单价不低于成本价,且不高于80元,某日该商场出售这种商品获得了14000元的利润,求该商品的售价?
(3)若某日该商场这种商品的销售量不少于500千克,求这一天该商场销售这种商品获得的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
(1)古希腊著名数学家欧几里得在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.其符号语言是:如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则:(1)AC=AB·AD;(2)BC=AB·BD;(3)CD = AD·BD;请你证明定理中的结论(1)AC = AB·AD.
(结论运用)
(2)如图2,正方形ABCD的边长为3,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
①求证:△BOF∽△BED;
②若![]() ,求OF的长.
,求OF的长.
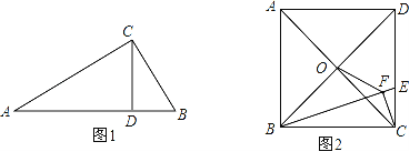
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点E.
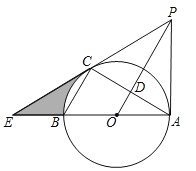
(1)求证:PC是⊙O的切线.
(2)若∠ABC=60°,AB=2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com