
 轴上,折叠边AD,使点D落在
轴上,折叠边AD,使点D落在 轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为
轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为 ,其中
,其中 >0.
>0.
 的式子表示);
的式子表示);  的值;
的值;  经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求
经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求 、
、 、
、 的值.
的值. 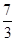 ;(3)
;(3)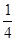 ,-1,12
,-1,12 即可求得
即可求得 、
、 的值,从而表示出点M的坐标,设对称轴交AD于G,即可表示出点G的坐标,求得AG、GM的长,再证得△AOB∽△AMG,根据相似三角形的性质即可求得结果.
的值,从而表示出点M的坐标,设对称轴交AD于G,即可表示出点G的坐标,求得AG、GM的长,再证得△AOB∽△AMG,根据相似三角形的性质即可求得结果.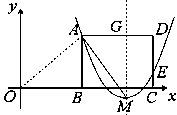
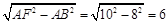 .
.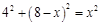 ,解得
,解得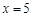
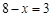
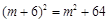 ,解得m=
,解得m=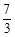 .
. 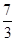 ;
;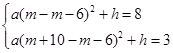 , 解得
, 解得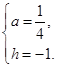
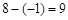
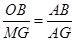 ,即
,即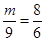


科目:初中数学 来源:不详 题型:解答题
 与y轴正半轴交于点C,连接BC、AC,CD是⊙
与y轴正半轴交于点C,连接BC、AC,CD是⊙ 的切线,AD⊥CD于点D,tan∠CAD=
的切线,AD⊥CD于点D,tan∠CAD= ,抛物线
,抛物线 过A、B、C三点.
过A、B、C三点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由; 轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
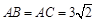 ,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.
,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.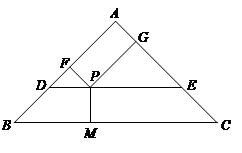
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
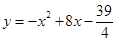 与
与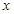 轴所围成的封闭图形染成红色,则在此红色内部区域及其边界上的
轴所围成的封闭图形染成红色,则在此红色内部区域及其边界上的查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

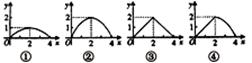
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
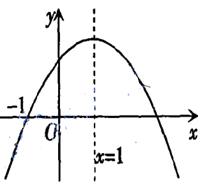
| A.ac>0 | B.当x>1时,y随x的增大而增大 |
| C.2a+b=1 | D.方程ax2+bx+c=0有一个根是x=3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
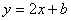 交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.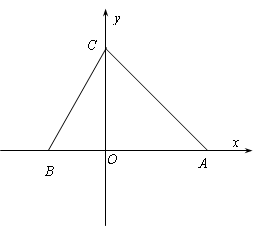
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.第8秒 | B.第10秒 | C.第12秒 | D.第15秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com