
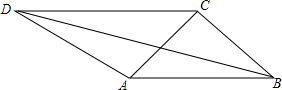
 如图,已知CA=CB,∠ACB=90°,∠CBD=30°,CD∥AB.
如图,已知CA=CB,∠ACB=90°,∠CBD=30°,CD∥AB.分析 (1)如图,作CE⊥CD且CE=CD;
(2)延长BC交DE于H,如图,根据等腰三角形的性质得∠CAB=∠CBA=45°,则∠1=45°-∠3=15°,再利用平行线的性质得∠2=∠1=15°,接着根据旋转的性质得CD=CE,∠DCE=90°,则∠CDE=∠CED=45°,易得∠BDH=60°,∠BHD=90°,然后根据等腰三角形的性质得DH=EH,于是利用线段垂直平分线的性质得BD=BE,则可判断△BDE为等边三角形,得到∠BED=60°,于是得到∠CEB=15°;
(3)作AF⊥CD于F,如图,设CH=DH=HE=a,则CD=$\sqrt{2}$a,在Rt△BDH中,利用含30度的直角三角形三边的关系得BD=2DH=2a,BH=$\sqrt{3}$DH=$\sqrt{3}$a,则BC=AC=($\sqrt{3}$-1)a,在等腰直角△ACF中,AF=CF=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{6}-\sqrt{2}}{2}$a,所以DF=CD-CF=$\frac{3\sqrt{2}-\sqrt{6}}{2}$a,于是在Rt△ADF中,利用勾股定理可计算出AD=($\sqrt{6}$-$\sqrt{2}$)a,所以$\frac{BD}{AD}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
解答 解:(1)如图1,CE为所作;
(2)延长BC交DE于H,如图2,
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∴∠1=45°-∠3=15°,
∵CD∥AB,
∴∠2=∠1=15°,
∵线段CD绕C点顺时针旋转90°到CE处,
∴CD=CE,∠DCE=90°,
∴∠CDE=∠CED=45°,
∴∠BDH=∠2+∠CDH=60°
∴∠BHD=90°,
∴CH⊥DE,
∴DH=EH,
∴BD=BE,
而∠BDE=60°,
∴△BDE为等边三角形,
∴∠BED=60°,
∴∠CEB=60°-45°=15°;
(3)作AF⊥CD于F,如图3,设CH=DH=HE=a,则CD=$\sqrt{2}$a,
在Rt△BDH中,BD=2DH=2a,BH=$\sqrt{3}$DH=$\sqrt{3}$a,
∴BC=$\sqrt{3}$a-a=($\sqrt{3}$-1)a,
∴AC=($\sqrt{3}$-1)a,
∵∠4=∠CAB=45°,
在Rt△ACF中,AF=CF=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$•($\sqrt{3}$-1)a=$\frac{\sqrt{6}-\sqrt{2}}{2}$a,
DF=CD-CF=$\sqrt{2}$a-$\frac{\sqrt{6}-\sqrt{2}}{2}$a=$\frac{3\sqrt{2}-\sqrt{6}}{2}$a,
在Rt△ADF中,AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{(\frac{\sqrt{6}-\sqrt{2}}{2}a)^{2}+(\frac{3\sqrt{2}-\sqrt{6}}{2}a)^{2}}$=$\sqrt{(8-4\sqrt{3}){a}^{2}}$=($\sqrt{6}$-$\sqrt{2}$)a,
∴$\frac{BD}{AD}$=$\frac{2a}{(\sqrt{6}-\sqrt{2})a}$=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了等腰直角三角形的性质和含30度的直角三角形三边的关系.本题的关键是证明BC与DE垂直,从而找到CD和BC的数量关系.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 奇奇妈妈买了一块正方形地毯,地毯上有“※”组成的图案,观察局部有如此规律:奇奇数※个数的方法是用“L”来划分,从右上角的1个开始,一层一层往外数,第一层1个,第二层3个,第三层5个…,这样她发现了连续奇数求和的方法.
奇奇妈妈买了一块正方形地毯,地毯上有“※”组成的图案,观察局部有如此规律:奇奇数※个数的方法是用“L”来划分,从右上角的1个开始,一层一层往外数,第一层1个,第二层3个,第三层5个…,这样她发现了连续奇数求和的方法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时.
如图,在小岛M处测得一艘渔船位于南偏东45°方向A处,该渔船从南向正北方向行驶一段距离后,到达位于小岛北偏东60°方向的B处,又航行了半小时到达C处,此时渔船在小岛的东北方向,渔船的速度为20海里/小时. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com