
����Ŀ����һ�߳�Ϊ40cm��������Ӳֽ�壬�����ʵ��ļ��ã��۳�һ�������κ��ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ��� 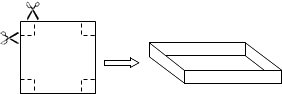
��1����ͼ������������Ӳֽ����ĽǸ���һ��ͬ����С�������Σ���ʣ�ಿ���۳�һ���ǵij����κ��ӣ� ��Ҫʹ�۳ɵij����κ��ӵĵ����Ϊ484cm2 �� ��ô�����������εı߳�Ϊ���٣�
���۳ɵij����κ��ӵIJ�����Ƿ������ֵ������У����������ֵ�ʹ�ʱ�����������εı߳������û�У�˵�����ɣ�
��2������������Ӳֽ������ܼ���һЩ���Σ��������ľ���������һ������������Ӳֽ��ı��ϣ�����ʣ�ಿ���۳�һ���иǵij����κ��ӣ����۳ɵ�һ�������κ��ӵı����Ϊ550cm2 �� ���ʱ�����κ��ӵij��������ߣ�ֻ���������Ҫ���һ���������
���𰸡�
��1���⣺��������������εı߳�Ϊxcm��
��40��2x��2=484��
��40��2x=��22��
���x1=31���������⣬��ȥ����x2=9��
������������εı߳�Ϊ9cm��
�ڲ���������ֵ��
�������С�����εı߳�Ϊacm�����ӵIJ����Ϊycm2��
��y��a�ĺ�����ϵΪ��y=4��40��2a��a��
��y=��8a2+160a��
��y=��8��a��10��2+800��
��a=10ʱ��y���=800��
���������������εı߳�Ϊ10cmʱ�������κ��ӵIJ�������Ϊ800cm2
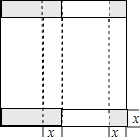
��2���⣺����ͼ��һ�ּ���ͼ�У�������ij����κ��ӵı߳�Ϊxcm��
2��40��2x����20��x��+2x��20��x��+2x��40��2x��=550��
��ã�x1=��35���������⣬��ȥ����x2=15��
������ij����κ��ӵı߳�Ϊ15cm��
40��2��15=10��cm����
20��15=5��cm����
��ʱ��������ӵij�Ϊ15cm����Ϊ10cm����Ϊ5cm��
����������1���ټ�������������εı߳�Ϊxcm����������ó���40��2x��2=484��������ɣ��ڼ�������������εı߳�Ϊacm�����ӵIJ����Ϊycm2 �� ��y��x�ĺ�����ϵΪ��y=4��40��2a��a�����ö��κ�����ֵ������ɣ���2����������ij����κ��ӵĸ�Ϊtcm�������۳ɵ�һ�������κ��ӵı����Ϊ550cm2 �� �ó���ʽ����������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У���![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��

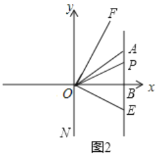
��1����![]() ������Ϊ ����
������Ϊ ����![]() ������Ϊ ��
������Ϊ ��
��2����ͼ1������![]() ��
��![]() ���ϣ�����
���ϣ�����![]() ��ʹ
��ʹ![]() �������
�������![]() �����ꣻ
�����ꣻ
��3����ͼ2��![]() ���߶�
���߶�![]() ����ֱ����һ���㣬����
����ֱ����һ���㣬����![]() ��
��![]() ƽ��
ƽ��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ������
������![]() ��ֱ��
��ֱ��![]() ���˶������У���̽��
���˶������У���̽��![]() ��
��![]() ��������ϵ����֤����
��������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD��ֱ��l��ֱ��AB��CD�ཻ�ڵ�E��F����P������EA�ϵ�һ�����㣨�������˵�E��������EPF��PF�۵���ʹ����E���ڵ�Q����
������PEF��48��,��Qǡ���������е�һ��ƽ������,���EFP�Ķ���Ϊ ��
������PEF��75�㣬��CFQ��![]() ��PFC�����EFP�Ķ�����
��PFC�����EFP�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ͷ�����Թ涨����6������Ϊ�ϸ�9������Ϊ���㣬�ס�������ͬѧ��һ�β��Գɼ����£�
�ɼ����֣� | 4 | 5 | 6 | 7 | 8 | 9 |
���飨�ˣ� | 1 | 2 | 5 | 2 | 1 | 4 |
���飨�ˣ� | 1 | 1 | 4 | 5 | 2 | 2 |
��1�������������ͳ�����ݣ��������ͼ�ͱ����������� 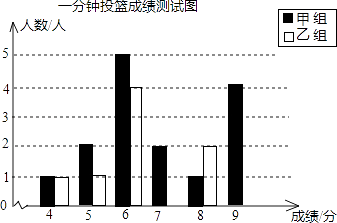
һ����Ͷ���ɼ�ͳ�Ʒ�������
ͳ���� | ƽ���� | ���� | ��λ�� | �ϸ��� | ������ |
���� | 2.56 | 6 | 80.0% | 26.7% | |
���� | 6.8 | 1.76 | 86.7% | 13.3% |
��2��������С����С�ϵ�һ�ζԻ���������ݣ�1���еı���д������֧��С�ϵĹ۵�����ɣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
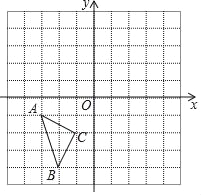
����Ŀ������ͼ��ʾ��ֱ������ϵ�У�ÿ��С�����DZ߳�Ϊ1�������Σ���ABC�Ķ�����ڸ���ϣ���A�������ǣ���3����1����
��1������ABC����x��ԳƵõ���A1B1C1��������A1B1C1����д����B1�����ꣻ
��2������A1B1C1ƽ�ƣ�ʹ��B1ƽ�Ƶ�B2��3��4������������A1B1C1ƽ�ƺ����A2B2C2����д��A2�����ꣻ
��3����֪��ABC����һ��D��a��b��������A2B2C2�еĶ�Ӧ��D2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC���������������ϣ�����AC��������y=x2��4x��2����A��B���㣮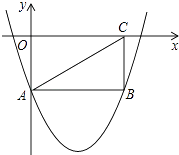
��1����A�����꼰�߶�AB�ij���
��2������P�ɵ�A������ÿ��1����λ���ٶ���AB�����B�ƶ���1����QҲ�ɵ�A������ÿ��7����λ���ٶ���AO��OC��CB�����B�ƶ���������һ���㵽���յ�ʱ��һ����Ҳֹͣ�ƶ�����P���ƶ�ʱ��Ϊt�룮
�ٵ�PQ��ACʱ����t��ֵ��
�ڵ�PQ��ACʱ�����������߶Գ�����һ��H����HOQ����POQ�����H���������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������е���1���ߣ����𱱻�վ�����������վ������15�����³�վ��2017��6��30�տ�ͨ��Ӫ����־�ż���ʡ��ʽ����������ʱ������15��վ����ͼ��ʾ��

ij�죬���������㳡վ��ʼ�����������ڵ�����վ����־Ը�߷���Aվ�³�ʱ������־Ը�߷���������Լ��������վ����Ϊ��������ij˳���¼���£���λ��վ����+5����2����6��+8��+3����4����9��+8
��1����ͨ������˵��Aվ����һվ��
��2��������վ֮��ľ���Ϊ1.3ǧ�ף����������־Ը�����ڼ���������н���·���Ƕ���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��������һ�������÷����������������ϵ�ש������ṹ��ͼ��ʾ.����ͼ�е����ݣ���λ��m��������������⣺
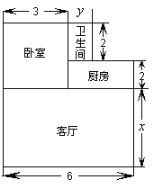
��1���ú�![]() ��
��![]() �Ĵ���ʽ��ʾ�����������
�Ĵ���ʽ��ʾ�����������
��2����![]() =5��
=5��![]() =
=![]() ����1m2��ש��ƽ������Ϊ80Ԫ����ô�̵�ש���ܷ���Ϊ����Ԫ��
����1m2��ש��ƽ������Ϊ80Ԫ����ô�̵�ש���ܷ���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���μӰ��ѡ��������ݽ������������������������ʱһ��һƱ���������㡢���á�һ�㡱��ѡһͶƱ����ͼ��7λ��ί��С�����ݽ���硱������ͳ��ͼ��ȫ��50λͬѧ��������Ʊ��ͳ��ͼ�� 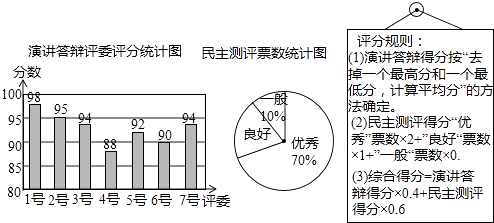
��1������ί��С���ݽ����������������Լ���������Ϊ�����á�Ʊ��������Բ�ĽǶ�����
��2����С�����ۺϵ÷��Ƕ��٣�
��3���ھ�ѡ�У�С�������������÷�Ϊ82�֣���������ۺϵ÷ֲ�С��С�����ۺϵ÷֣������ݽ����÷�����Ҫ���ٷ֣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com