练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．A、B两厂在公路的同侧，现欲在公路边建一货场C．
    （1）若要使货场到两厂的距离相等，请在图1中作出此时货场的位置．
    （2）若要求所修公路（即A、B两厂到货场的距离之和）最短，请在图2中作出货场的位置．（用尺规作图，保留作图痕迹，不必写作法）

    分析 （1）直接利用线段垂直平分线的性质以及其作法得出符合题意的答案；
    （2）利用轴对称求最短路线的方法得出货场的位置．

    解答 解：（1）如图1所示：点C即为所求；

    （2）如图2所示：点C即为所求．

    点评 此题主要考查了应用设计与作图，正确掌握基本作图方法是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．已知△ABC的三边长分别是5cm，12cm，13cm，则△ABC的面积是（　　）
    A．30cm2B．78cm2C．$\frac{65}{2}$cm2D．60cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．直线MN与直线PQ相交于O，点A在射线OP上运动，点B 在射线OM上运动．
    （1）如图1，若∠AOB=80°，已知AE、BE分别是∠BAO和∠ABO的角平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
    （2）如图2，若∠AOB=80°，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，AD、BC的延长线交于点F，点A、B在运动的过程中，∠F=50°；DE、CE又分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小也不发生变化，其大小为：∠CED=65°．
    （3）如图3，若∠AOB=90°，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F，则∠EAF=90°；
    （4）如图3，若AF，AE分别是∠GAO，∠BAO的角平分线，∠AOB=90°，在△AEF中，如果有一个角是另一个角的4倍，则∠ABO的度数=36°或45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图所示，一棵大树在一次强烈的地震中于C处折断倒下，树顶落在地面B处，测得B处与树的底端A相距25米，∠ABC=24°．
    （1）求大树折断倒下部分BC的长度；（精确到1米）
    （2）问大树在折断之前高多少米？（精确到1米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图是某种货车自动卸货时的示意图，AC是水平汽车底盘，OB是液压举升杠杆，货车卸货时车厢AB与底盘AC的夹角为30°，举升杠杆OB与底盘AC的夹角为75°，已知O与A的距离为4米，试求货车卸货时举升杠杆OB的长（$\sqrt{2}≈1.414$，精确到0.01米）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．下面两个图中，点A、B、C均在⊙O上，∠C=40°，请根据下列条件，仅用无刻度的直尺各画一个直角三角形，使其一个顶点为A，且一个内角度数为40°．
    （1）在图1中，点O在∠C外部；
    （2）在图2中，点O在∠C内部且点D在弦AB上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，△ABC的∠BAC的平分线AD被EF垂直平分，且E、F分别在AB，AC上，求证：四边形AEDF是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

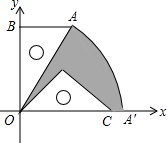    2．已知：如图，有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把该套三角板放置在平面直角坐标系中，且AB=3．
    （1）若双曲线的一个分支恰好经过点A，求双曲线的解析式；
    （2）若把含30°的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好与x轴重叠，点A落在点A′，试求图中阴影部分的面积（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，已知线段a，b．
    （1）按下列要求作图：
    ①用直尺和圆规作Rt△ABC，使∠C=90°，BC=a，AC=b；
    ②用直尺和圆规作AB边的中垂线，分别交AC，AB于D，E两点，连结BD．
    （2）若∠A=38°，求∠CBD的度数；
    （3）若a=3，b=4，求DE的长．

    查看答案和解析>>

    同步练习册答案