
【题目】如图抛物线y=ax2+bx+c的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
求出抛物线与y轴的交点C的坐标,即可求出点B的坐标,从而得出x=-2和x=-c为一元二次方程ax2+bx+c=0的解,根据根与系数的关系,列出等式即可判断①和②;将x=-c代入一元二次方程中,然后变形即可判断③;根据抛物线的图象判断出a、b的符号即可判断④.
解:将x=0代入解析式中可得y=c
∴点C的坐标为(0,c),
由图可知c<0
∵OB=OC
∴点B的坐标为(-c,0)
∴x=-2和x=-c为一元二次方程ax2+bx+c=0的解
根据根与系数的关系可得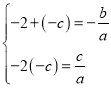
解第二个等式可得:![]() ,故②正确;
,故②正确;
将![]() 代入第一个等式,可得
代入第一个等式,可得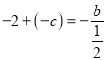
变形,得![]() ,故①正确;
,故①正确;
将x=-c代入一元二次方程ax2+bx+c=0中,得
ac2-bc+c=0
将等式的两边同时除以c,可得
ac-b+1=0
移项,得![]() ,故③正确;
,故③正确;
由抛物线可知:抛物线的开口向上,对称轴在y轴左侧
∴a>0,a和b同号
∴b>0
∴a+b>0
∵c<0
∴![]() ,故④正确.
,故④正确.
正确的有4个
故选D.


科目:初中数学 来源: 题型:
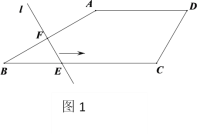
【题目】如图1,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直线
,直线![]() .当直线
.当直线![]() 沿射线
沿射线![]() 方向,从点
方向,从点![]() 开始向右平移时,直线
开始向右平移时,直线![]() 与四边形
与四边形![]() 的边分别相交于点
的边分别相交于点![]() 、
、![]() .设直线
.设直线![]() 向右平移的距离为
向右平移的距离为![]() ,线段
,线段![]() 的长为
的长为![]() ,且
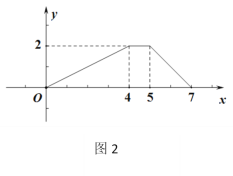
,且![]() 与
与![]() 的函数关系如图2所示,则四边形
的函数关系如图2所示,则四边形![]() 的周长是_____.
的周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
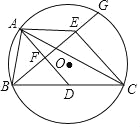
【题目】如图,△ABC内接于⊙O,AD是△ABC的中线,AE∥BC,射线BE交AD于点F,交⊙O于点G,点F是BE的中点,连接CE.
(1)求证:四边形ADCE为平行四边形;
(2)若BC=2AB,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形Ⅰ的面积为6,矩形Ⅱ中的三条边总长为6,则下列说法不正确的是( )
A.矩形Ⅰ中一组邻边的长满足反比例函数关系
B.矩形Ⅰ中一组邻边的长可能是3+![]() 和3﹣
和3﹣![]()
C.矩形Ⅰ的周长不可能是8
D.矩形Ⅱ的最大面积是3
查看答案和解析>>
科目:初中数学 来源: 题型:
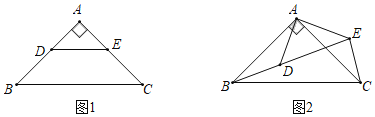
【题目】把两个等腰直角△ABC和△ADE按如图1所示的位置摆放,将△ADE绕点A按逆时针方向旋转,如图2,连接BD,EC,设旋转角为α(0°<α<360°)
(1)当DE⊥AC时,AD与BC的位置关系是 ,AE与BC的位置关系是 ;
(2)如图2,当点D在线段BE上时,求∠BEC的度数;
(3)当旋转角α= 时,△ABD的面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
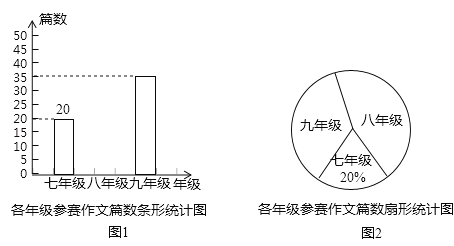
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
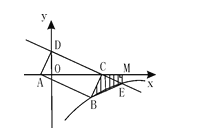
【题目】如图,直线y=-![]() x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=![]() (k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
(k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.

(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F=![]() ,CD=a,请用a表示⊙O的半径;
,CD=a,请用a表示⊙O的半径;
(3)求证:GF2﹣GB2=DFGF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com