
分析 (1)利用配方法或顶点坐标公式即可解决问题.
(2)欲证明二次函数y=x2-(2k+1)x+k2+k(k>0)的图象与x轴有两个不同的交点,只要证明△>0即可.
(3)由题意正整数a,b,c恰好是一个三角形的三边长,推出a的最小值为2,所以对称轴x=-$\frac{-(2k+1)}{2}$<$\frac{5}{2}$时,当a<b<c时,都有y1<y2<y3,解不等式即可解决问题.
解答 (1)解:当k=$\frac{1}{2}$时,这个二次函数的解析式为y=x2-2x+$\frac{3}{4}$,
∵y=x2-2x+$\frac{3}{4}$=(x-1)2-$\frac{1}{4}$,
∴这个二次函数的顶点坐标为(1,-$\frac{1}{4}$);
(2)证明:对于二次函数y=x2-(2k+1)x+k2+k(k>0),
∵△=[-(2k+1)]2-4k2-4k=1>0,
∴二次函数y=x2-(2k+1)x+k2+k(k>0)的图象与x轴有两个不同的交点.
(3)∵正整数a,b,c恰好是一个三角形的三边长,
∴a的最小值为2,
∴对称轴x=-$\frac{-(2k+1)}{2}$<$\frac{5}{2}$时,当a<b<c时,都有y1<y2<y3,
∴k<2,∵k>0,
∴0<k<2时,满足条件.
故答案为0<k<2.
点评 本题考查抛物线与x轴的交点、二次函数与一元二次方程的关系等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,所以中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
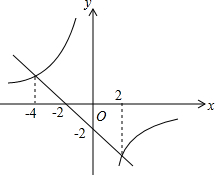 若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )
若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示,则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为( )| A. | 0<x≤2或x≤-4 | B. | -4≤x<0或x≥2 | C. | $-2\sqrt{2}$≤x<0或x$≥2\sqrt{2}$ | D. | x$≤-2\sqrt{2}$或0$<x≤2\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲班 | 0.1 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
| 乙班 | 0.8 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
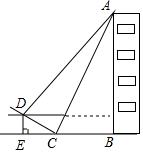 如图,我市某中学数学兴趣小组决定测量一下本校教学楼AB的高度,他们在楼梯底部C处测得∠ACB=60°,∠DCE=30°;沿楼梯向上走到D处测得∠ADF=45°,D到地面BE的距离DE为3米.求教学楼AB的高度.(站果精确列1米,参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7)
如图,我市某中学数学兴趣小组决定测量一下本校教学楼AB的高度,他们在楼梯底部C处测得∠ACB=60°,∠DCE=30°;沿楼梯向上走到D处测得∠ADF=45°,D到地面BE的距离DE为3米.求教学楼AB的高度.(站果精确列1米,参考数据:$\sqrt{2}≈$1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
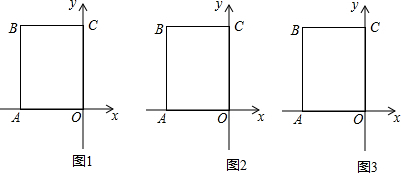
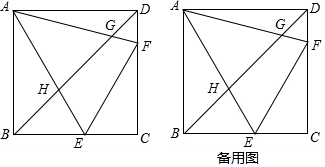 如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.
如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com