
 已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P($\frac{1}{2}$,n),Q(4,m)两点,且tan∠BOP=$\frac{1}{16}$:
已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P($\frac{1}{2}$,n),Q(4,m)两点,且tan∠BOP=$\frac{1}{16}$:分析 (1)过P作PC⊥y轴于C,由P($\frac{1}{2}$,n),得到OC=n,PC=$\frac{1}{2}$,根据三角函数的定义得到P($\frac{1}{2}$,8),于是得到反比例函数的解析式为y=$\frac{4}{x}$,Q(4,1),解方程组即可得到直线的函数表达式为y=-2x+9;
(2)过Q作OD⊥y轴于D,于是得到S△POQ=S四边形PCDQ=$\frac{63}{4}$.
解答 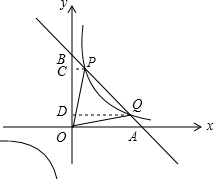 解:(1)过P作PC⊥y轴于C,
解:(1)过P作PC⊥y轴于C,
∵P($\frac{1}{2}$,n),
∴OC=n,PC=$\frac{1}{2}$,
∵tan∠BOP=$\frac{1}{16}$,
∴n=8,
∴P($\frac{1}{2}$,8),
设反比例函数的解析式为y=$\frac{a}{x}$,
∴a=4,
∴反比例函数的解析式为y=$\frac{4}{x}$,
∴Q(4,1),
把P($\frac{1}{2}$,8),Q(4,1)代入y=kx+b中得$\left\{\begin{array}{l}{8=\frac{1}{2}k+b}\\{1=4k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-2}\\{b=9}\end{array}\right.$,
∴直线的函数表达式为y=-2x+9;
(2)过Q作OD⊥y轴于D,
则S△POQ=S四边形PCDQ=$\frac{1}{2}$($\frac{1}{2}$+4)×(8-1)=$\frac{63}{4}$.
点评 本题考查了反比例函数与一次函数的交点问题,反比例函数图象上点的坐标特征,利用待定系数法求反比例函数和一次函数的解析式,正切函数的定义,难度适中,利用数形结合是解题的关键.


科目:初中数学 来源: 题型:解答题
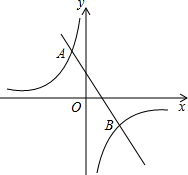 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A(-2,6)和点B(4,n).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A(-2,6)和点B(4,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
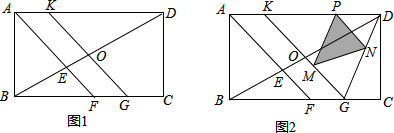
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
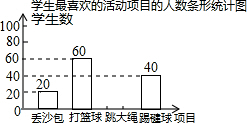 我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:| 项目 | 学生数(名) | 百分比 |
| 丢沙包 | 20 | 10% |
| 打篮球 | 60 | p% |
| 跳大绳 | n | 40% |
| 踢毽球 | 40 | 20% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{160}{4x}$-$\frac{160}{5x}$=30 | B. | $\frac{160}{4x}$-$\frac{160}{5x}$=$\frac{1}{2}$ | C. | $\frac{160}{5x}$-$\frac{160}{4x}$=$\frac{1}{2}$ | D. | $\frac{160}{4x}$+$\frac{160}{5x}$=30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com