
【题目】在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0),点P是直线AB上的一个动点,记点P关于y轴对称的点为P′.
(1)当b=3时(如图1),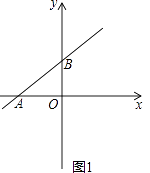
①求直线AB的函数表达式.
(2)②在x轴上找一点Q(点O除外),使△APQ与△AOB全等,直接写出点Q的所有坐标
(3)若点P在第一象限(如图2),设点P的横坐标为a,作PC⊥x轴于点C,连结AP′,CP′.当△ACP′是以点P′为直角顶点的等腰直角三角形时,求出a,b的值.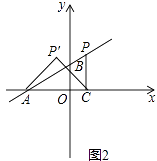
(4)当线段OP′恰好被直线AB垂直平分时(如图3),直接写出b= . 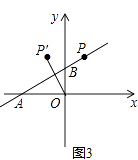
【答案】
(1)
解:设直线AB的函数表达式为y=kx+b,
∵点A的坐标是(﹣4,0),点B的坐标是(0,3)
∴有 ![]() ,解得:
,解得: ![]() .
.
故直线AB的函数表达式为y= ![]() x+3.
x+3.
(2)(﹣9,0)、(﹣8,0)或(1,0)
(3)
解:过P′作PD⊥x轴于点D,如图所示.
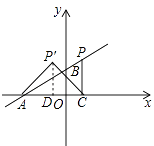
∵点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0),
∴直线AB的斜率为 ![]() =
= ![]() ,
,
即直线AB的解析式为y= ![]() x+b.
x+b.
∵点P在直线AB上,
∴点P的坐标为(a, ![]() a+b),则点P′的坐标为(﹣a,
a+b),则点P′的坐标为(﹣a, ![]() a+b),点C的坐标为(a,0),点D的坐标为(﹣a,0),
a+b),点C的坐标为(a,0),点D的坐标为(﹣a,0),
∴P′D= ![]() a+b,AC=a+4,AD=4﹣a.
a+b,AC=a+4,AD=4﹣a.
∵点P为第一象限的点,
∴a>0.
∵△ACP′是以点P′为直角顶点的等腰直角三角形,
∴有 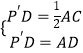 ,即
,即 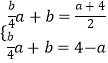 ,
,
解得: ![]()
(4)![]()
【解析】解:(1)①设直线AB的函数表达式为y=kx+b,
∵点A的坐标是(﹣4,0),点B的坐标是(0,3)
∴有 ![]() ,解得:
,解得: ![]() .
.
故直线AB的函数表达式为y= ![]() x+3.
x+3.
②∵点P是直线AB上的一个动点,点Q为x轴上一点(点O除外),
∴设点Q的坐标为(m,0),∠PAQ=∠BAO,
∴AQ=|m+4|.
在Rt△AOB中,AO=4,BO=3,AB= ![]() =5.
=5.
△APQ与△AOB全等有两种情况:
当AQ=AO时,即|m+4|=4,
解得:m=0(舍去),或m=﹣8,
此时点Q的坐标为(﹣8,0);
当AQ=AB时,即|m+4|=5,
解得:m=﹣9,或m=1,
此时点Q的坐标为(﹣9,0)或(1,0).
综上所述:点Q的所有坐标为(﹣9,0),(﹣8,0)或(1,0).
所以答案是:(﹣9,0),(﹣8,0)或(1,0).(4)由(3)可知:点P的坐标为(a, ![]() a+b),则点P′的坐标为(﹣a,
a+b),则点P′的坐标为(﹣a, ![]() a+b),直线AB的解析式为y=
a+b),直线AB的解析式为y= ![]() x+b.
x+b.
则OP′的中点坐标为(﹣ ![]() ,
, ![]() ),直线OP′的斜率为
),直线OP′的斜率为 ![]() =﹣
=﹣ ![]() ﹣
﹣ ![]() .
.
∵线段OP′恰好被直线AB垂直平分,
∴有  ,
,
解得: 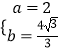 ,或
,或 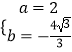 (舍去).
(舍去).
所以答案是: ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
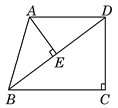
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强与小刚两位同学在学习“概率”时,做抛骰子(均匀立方体形状)试验,他们共抛了54次,出现不同向上点数的次数如下表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)小强说:“根据试验,一次试验中出现向上点数为5的概率最大.”小刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断小强和小刚说法的对错.
(3)如果小强与小刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从标号分别为1,2,3,4,5的5张卡片中,随机抽取1张.下列事件中,必然事件是【 】
A.标号小于6 B.标号大于6 C.标号是奇数 D.标号是3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.过一点有且只有一条直线与已知直线垂直
B.过直线外一点有且只有一条直线与已知直线平行
C.垂于同一条直线的两条直线平行
D.如果两个角的两边分别平行,那么这两个角一定相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF, 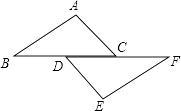
(1)求证:AB=EF.
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com