
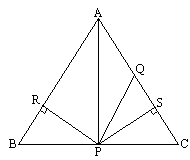
如图,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S.则三个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP中
[ ]
|
答案: (B)解:∵ PS⊥AC于S,PR⊥AB于R,PR=PS,∴ AP是∠BAC的平分线.∴∠ RAP=∠SAP.∵ AP=AP,∴△ARP≌△ASP.∴ AS=AR.∴①正确.∵ AQ=PQ,∴∠QPA=∠QAP.∴∠ QPA=∠BAP.∴ QP∥AR.∴②正确.∵如果△ BRP≌△QSP成立,则∠B=∠SQP,而∠SQP=∠CAB,即如果△BRP≌△QSP,则必须有∠B=∠CAB这一条件,而已知条件不能确定这两个角相等.∴③不一定正确,因此正确选题为 (B). |
|
从条件“ PR⊥AB于R、PS⊥AC于S、PR=PS”易知,AP是∠BAC的平分线,利用角平分线的性质及全等的判定性质,就能推出①、②正确,否定③可用特殊三角形来说明. |


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com