

分析 (1)根据平行线的判定与性质填写即可;
(2)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;
(3)画出图形(分两种情况①点P在BA的延长线上,②点P在AB的延长线上),根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
解答 解:(1)过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD.(平行于同一条直线的两条直线平行)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(两直线平行同旁内角互补)
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.(等量代换)
故答案为:平行于同一条直线的两条直线平行;两直线平行同旁内角互补;等量代换.
(2)∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,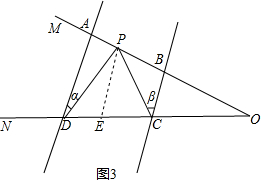
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(3)当P在BA延长线时,
过P作PE∥AD交CD于E,
同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠β-∠α;
当P在AB延长线时,
同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠α-∠β.
点评 本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,题目是一道比较典型的题目,难度适中.


科目:初中数学 来源: 题型:解答题
 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长)用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x m.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长)用26m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=x m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,若横坐标、纵坐标均为整数点称为格点,若一个多边形的顶点都是格点,则称为格点多边形.记格点多边形的面积为S,其内部的格点数记为n,边界上的格点数记为l,例如图中△ABC是格点三角形,对应的S=1,n=0,l=4.
在平面直角坐标系中,若横坐标、纵坐标均为整数点称为格点,若一个多边形的顶点都是格点,则称为格点多边形.记格点多边形的面积为S,其内部的格点数记为n,边界上的格点数记为l,例如图中△ABC是格点三角形,对应的S=1,n=0,l=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com