
 若实数a,b,c在数轴上的位置如图,
若实数a,b,c在数轴上的位置如图,| a2 |
| c2 |
| (a-c)2 |
| a2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 6 |
5+2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
| 2 |
| 6 |
5+2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
所谓配方法其实就是逆用完全平方公式,即![]() .该方法在数、式、方程等多方面应用非常广泛,如
.该方法在数、式、方程等多方面应用非常广泛,如![]()
![]()
![]() ;
;![]()
![]() =
=![]() 等等.请你用配方法解决以下问题:
等等.请你用配方法解决以下问题:
1.解方程:![]() ;(不能出现形如
;(不能出现形如![]() 的双重二次根式)
的双重二次根式)
2.)若![]() ,解关于x的一元二次方程
,解关于x的一元二次方程![]() ;
;
3.求证:不论m为何值,解关于x的一元二次方程![]() 总有两个不等实数根
总有两个不等实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
 .该方法在数、式、方程等多方面应用非常广泛,如
.该方法在数、式、方程等多方面应用非常广泛,如

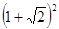 ;
;
 =
= 等等.请你用配方法解决以下问题:
等等.请你用配方法解决以下问题: ;(不能出现形如
;(不能出现形如 的双重二次根式)
的双重二次根式) ,解关于x的一元二次方程
,解关于x的一元二次方程 ;
; 总有两个不等实数根
总有两个不等实数根查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com