
已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
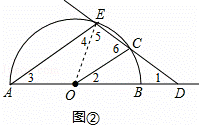
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
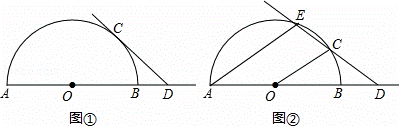
解:(1)如图①,连接OC,
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45°;
(2)如图②,连接OE.
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°﹣2x.
①AE=OD.理由如下:
在△AOE与△OCD中,
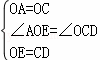
∴△AOE≌△OCD(SAS),
∴AE=OD.
②∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
已知抛物线y=x2﹣(k+2)x+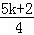 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
(1)求证:无论k取何实数值,抛物线总与x轴有两个不同的交点;
(2)抛物线于x轴交于点A、B,直线与x轴交于点C,设A、B、C三点的横坐标分别是x1、x2、x3,求x1•x2•x3的最大值;
(3)如果抛物线与x轴的交点A、B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D、E,直线AD交直线CE于点G(如图),且CA•GE=CG•AB,求抛物线的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com