
【题目】某中学为了美化校园环境,计划购进桂花树和黄桷树两种树苗共200棵,现通过调查了解到:若购进15棵桂花树和6棵黄桷树共需600元,若购进12棵桂花树和5棵黄桷树共需490元.
(1)求购进的桂花树和黄桷树的单价各是多少元?
(2)已知甲、乙两个苗圃的两种树苗销售价格和上述价格一样,但有如下优惠:甲苗圃:每购买一棵黄桷树送两棵桂花树,购买的其它桂花树打9折.乙苗圃:购买的黄桷树和桂花树都打7折.设购买黄桷树x棵,y1和y2分别表示到甲、乙两个苗圃中购买树苗所需总费用,求出y1和y2关于x的函数表达式;
(3)现在,学校根据实际需要购买的黄桷树的棵数不少于35棵且不超过40棵,请设计一种购买方案,使购买的树苗所花费的总费用最少.最少费用是多少?
【答案】(1)购进的桂花树为20元/棵,黄桷树为50元/棵;(2)y1=﹣4x+3600,y2=21x+2800;(3)到甲苗圃购买40棵黄桷树,160棵桂花树时,费用最小,最少费用为3440元.
【解析】
(1)设购进的桂花树为x元/棵,黄桷树为y元/棵,由题意可列方程组,可求得答案;
(2)利用题目中所给的方案,分别表示y1、y2即可;
(3)令y1=y2,可求得x=32,利用一次函数的增减性,进行判断即可.
(1)设购进的桂花树为x元/棵,黄桷树为y元/棵,
由题意![]() ,解得
,解得![]() ,
,
答:购进的桂花树为20元/棵,黄桷树为50元/棵;
(2)由题意可得y1=50x+(200﹣x﹣2x)×20×90%,即y1=﹣4x+3600,
y2=[50x+(200﹣x)×20]×70%,即y2=21x+2800;
(2)∵当y1=y2时,即﹣4x+3600=21x+2800,解得x=32,
∴当x=32时,y1=y2,即当x=32时,到两家苗圃购买费用一样,
∵y1随x的增大而减小,y2可随x的增大而增大,
∴选择到甲苗圃购买,
∵35≤x≤40,
∴当x=40时,费用最少为:y=﹣4×40+3600=3440元,
即到甲苗圃购买40棵黄桷树,160棵桂花树时,费用最小,最少费用为3440元.


科目:初中数学 来源: 题型:
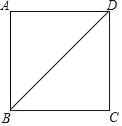
【题目】如图,正方形ABCD中,BD为对角线.
(1)尺规作图:作CD边的垂直平分线EF,交CD于点E,交BD于点F(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若AB=4,求△DEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
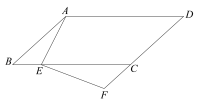
【题目】如图,在□ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
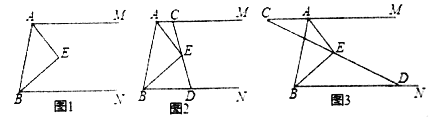
【题目】如图,![]() 、
、![]() 、
、![]() 的平分线交于
的平分线交于![]() .
.
(1)![]() 是什么角?(直接写结果)
是什么角?(直接写结果)
(2)如图2,过点![]() 的直线交射线
的直线交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,观察线段
,观察线段![]() ,你有何发现?并说明理由.
,你有何发现?并说明理由.
(3)如图2,过点![]() 的直线交射线
的直线交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(4)如图3,过点![]() 的直线交射线
的直线交射线![]() 的反向延长线于点
的反向延长线于点![]() ,交射线
,交射线![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,淇淇一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,C地恰好位于A地正东方向上,则( )
①B地在C地的北偏西50°方向上;
②A地在B地的北偏西30°方向上;
③cos∠BAC=![]() ;
;
④∠ACB=50°.其中错误的是( )
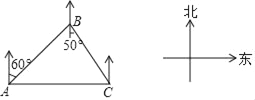
A. ①② B. ②④ C. ①③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=120°,∠C=80°.将△BMN沿着MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠F的度数为( )
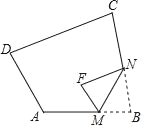
A. 70° B. 80° C. 90° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x﹣5与x轴交于A,B两点(电B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求A,B,C三点的坐标及抛物线的对称轴.
(2)如图1,点E(m,n)为抛物线上一点,且2<m<5,过点E作EF∥x轴,交抛物线的对称轴于点F,作EH⊥x轴于点H,求四边形EHDF周长的最大值.
(3)如图2,点P为抛物线对称轴上一点,是否存在点P,使以点P,B,C为顶点的三角形是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
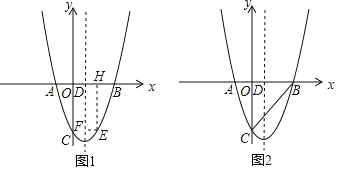
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com