
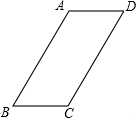
 如图所示是一块平行四边形的铁片ABCD,且AB=2AD,现在想用这块铁片截一个直角三角形,并要求斜边与AB重合,面积最大,能否截出符合条件的三角形?如果能截出,画出截线;如果不能截出,说明理由.
如图所示是一块平行四边形的铁片ABCD,且AB=2AD,现在想用这块铁片截一个直角三角形,并要求斜边与AB重合,面积最大,能否截出符合条件的三角形?如果能截出,画出截线;如果不能截出,说明理由.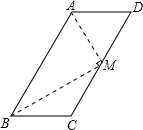 解:取CD的中点M,连接AM,BM.
解:取CD的中点M,连接AM,BM. CD,AD=DM,BC=CM.
CD,AD=DM,BC=CM.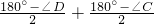 =180°-
=180°- (∠C+∠D).
(∠C+∠D). ×180°=90°,
×180°=90°,

科目:初中数学 来源: 题型:
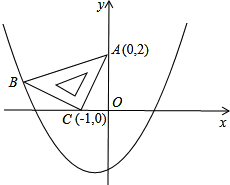 两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.
两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:013
如图所示,某村准备在一块长方形的土地上修一条供灌溉的水渠道(水渠两岸是平行的),考虑各方面因素有三种设计方案,方案图纸出来后,有人提出要首先满足少占耕地的条件.按如下图纸推算,除水渠道占的面积外,剩下的土地面积分别用 表示,有以下四种结论,其中正确的是
表示,有以下四种结论,其中正确的是
[ ]






查看答案和解析>>
科目:初中数学 来源: 题型:013
如图所示,某村准备在一块长方形的土地上修一条供灌溉的水渠道(水渠两岸是平行的),考虑各方面因素有三种设计方案,方案图纸出来后,有人提出要首先满足少占耕地的条件.按如下图纸推算,除水渠道占的面积外,剩下的土地面积分别用 表示,有以下四种结论,其中正确的是
表示,有以下四种结论,其中正确的是
[ ]






查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.
两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.查看答案和解析>>
科目:初中数学 来源:2009年浙江省绍兴市绍兴县王坛镇中数学中考模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com