
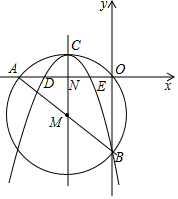
 如图,在平面直角坐标系中,圆M经过原点O,且与x轴、y轴分别相交于A(-8,0),B(0,-6)两点.
如图,在平面直角坐标系中,圆M经过原点O,且与x轴、y轴分别相交于A(-8,0),B(0,-6)两点.分析 (1)利用待定系数法可求出直线AB的解析式;
(2)先利用勾股定理计算出AB=10,再根据圆周角定理得到AB为⊙M的直径,则点M为AB的中点,M(-4,-3),则可确定C(-4,2),然后利用顶点式求出抛物线解析式;
(3)通过解方程-$\frac{1}{2}$(x+4)2+2=0得到D(-6,0),E(-2,0),利用S△ABC=S△ACM+S△BCM,可求出S△ABC=10,设P(t,-$\frac{1}{2}$t2-4t-6),所以$\frac{1}{2}$•(-2+6)•|-$\frac{1}{2}$t2-4t-6|=$\frac{1}{10}$•20,然后解绝对值方程求出t即可得到P点坐标.
解答 解:(1)设直线AB的函数解析式为y=kx+b,
把A(-8,0),B(0,-6)代入得$\left\{\begin{array}{l}{-8k+b=0}\\{b=-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=-6}\end{array}\right.$,
所以直线AB的解析式为y=-$\frac{3}{4}$x-6;
(2)在Rt△AOB中,AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵∠AOB=90°,
∴AB为⊙M的直径,
∴点M为AB的中点,M(-4,-3),
∵MC∥y轴,MC=5,
∴C(-4,2),
设抛物线的解析式为y=a(x+4)2+2,
把B(0,-6)代入得16a+2=-6,解得a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$(x+4)2+2,即y=-$\frac{1}{2}$x2-4x-6;
(3)存在.
当y=0时,-$\frac{1}{2}$(x+4)2+2=0,解得x1=-2,x2=-4,
∴D(-6,0),E(-2,0),
S△ABC=S△ACM+S△BCM=$\frac{1}{2}$•8•CM=20,
设P(t,-$\frac{1}{2}$t2-4t-6),
∵S△PDE=$\frac{1}{10}$S△ABC,
∴$\frac{1}{2}$•(-2+6)•|-$\frac{1}{2}$t2-4t-6|=$\frac{1}{10}$•20,
即|-$\frac{1}{2}$t2-4t-6|=1,
当-$\frac{1}{2}$t2-4t-6=1,解得t1=-4+$\sqrt{6}$,t2=-4-$\sqrt{6}$,此时P点坐标为(-4+$\sqrt{6}$,1)或(-4-$\sqrt{6}$,1)
当-$\frac{1}{2}$t2-4t-6=-1,解得t1=-4+$\sqrt{2}$,t2=-4-$\sqrt{2}$;此时P点坐标为(-4+$\sqrt{2}$,-1)或(-4-$\sqrt{2}$,-1)
综上所述,P点坐标为(-4+$\sqrt{6}$,1)或(-4-$\sqrt{6}$,1)或(-4+$\sqrt{2}$,-1)或(-4-$\sqrt{2}$,-1)时,使得S△PDE=$\frac{1}{10}$S△ABC.
点评 本题考查了圆的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和圆周角定理;会利用待定系数法求函数解析式;会解一元二次方程;记住三角形面积公式.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米.
如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
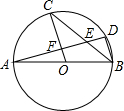 如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:
如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:| A. | ①③⑤ | B. | ②③④ | C. | ②④⑤ | D. | ①③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点P在⊙O外 | B. | 点P在⊙O内 | C. | 点P在⊙O上 | D. | 点P在⊙O外或⊙O上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com