
【题目】如图,在ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.
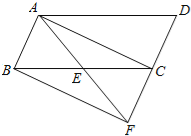
(1)求证:CF=CD;
(2)若AF平分∠BAD,连接DE,试判断DE与AF的位置关系,并说明理由.
【答案】(1)见解析(2)DE⊥AF
【解析】
试题(1)根据平行四边形的性质可得到AB∥CD,从而可得到AB∥DF,根据平行线的性质可得到两组角相等,已知点E是BC的中点,从而可根据AAS来判定△BAE≌△CFE,根据全等三角形的对应边相等可证得AB=CF,进而得出CF=CD;
(2)利用全等三角形的判定与性质得出AE=EF,再利用角平分线的性质以及等角对等边求出DA=DF,利用等腰三角形的性质求出即可.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
则在△BAE和△CFE中,
![]() ,
,
∴△BAE≌△CFE(AAS),
∴AB=CF,
∴CF=CD;
(2)解:DE⊥AF,
理由:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵∠BAF=∠F,
∴∠DAF=∠F,
∴DA=DF,
又由(1)知△BAE≌△CFE,
∴AE=EF,
∴DE⊥AF.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
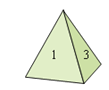
【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数.
(1)同时抛掷两个这样的四面体,它们着地一面的数字相同的概率是多少?
(2)现在有一张周杰伦演唱会的门票,小敏和小亮用抛掷这两个四面体的方式来决定谁获得门票,规则是:同时抛掷这两个四面体,如果着地一面的数字之积为奇数小敏胜;如果着地一面的数字之积为偶数小亮胜(胜方获得门票),如果是你,你愿意充当小敏还是小亮,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮为下周日计划了三项活动,分别是看电影(记为A)、去郊游(记为B)、去图书馆(记为C).他们各自在这三项活动中任选一个,每项活动被选中的可能性相同.
(1)小明选择去郊游的概率为多少;
(2)请用树状图或列表法求小明和小亮的选择结果相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
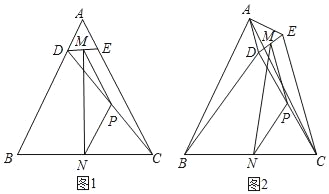
【题目】如图1,△ABC中,AB=AC=6,BC=4,点D、E分别在边AB、AC上,且AD=AE=1,连接DE、CD,点M、N、P分别是线段DE、BC、CD的中点,连接MP、PN、MN.
(1)求证:△PMN是等腰三角形;
(2)将△ADE绕点A逆时针旋转,
①如图2,当点D、E分别在边AC两侧时,求证:△PMN是等腰三角形;
②当△ADE绕点A逆时针旋转到第一次点D、E、C在一条直线上时,请直接写出此时BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
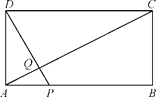
【题目】如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个一次函数l1、l2的图象如图:
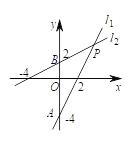
(1)分別求出l1、l2两条直线的函数关系式;
(2)求出两直线与y轴围成的△ABP的面积;
(3)观察图象:请直接写出当x满足什么条件时,l1的图象在l2的下方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com