
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C顺时针旋转60°得△ADC,连接OD.当AO=5,BO=4,α=150°时,则CO的长为_________.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为B(2,1),且过点A(0,2),直线y=x与抛物线交于点D,E(点E在对称轴的右侧),抛物线的对称轴交直线y=x于点C,交x轴于点G,EF⊥x轴,垂足为F,点P在抛物线上,且位于对称轴的右侧,PQ⊥x轴,垂足为点Q,△PCQ为等边三角形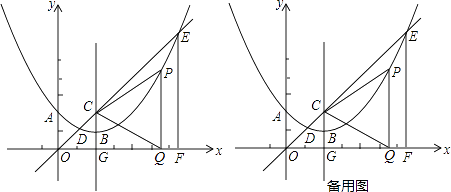
(1)求该抛物线的解析式;
(2)求点P的坐标;
(3)求证:CE=EF;
(4)连接PE,在x轴上点Q的右侧是否存在一点M,使△CQM与△CPE全等?若存在,试求出点M的坐标;若不存在,请说明理由.[注:3+2 ![]() =(
=( ![]() +1)2].
+1)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
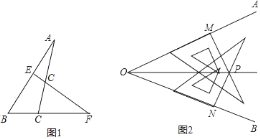
【题目】(1)如图1在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=45°,
∠F=30°,∠CGF=70°,求∠A的度数.
(2)利用三角板也能画出一个角的平分线,画法如下:①利用三角板在∠AOB的两边上分
别取OM=ON:②分别过点M、N画OM、ON的垂线,交点为![]() ;③画射线OP,所以射线OP为∠AOB的角平分线,请你评判这种作法的正确性并说明理由.
;③画射线OP,所以射线OP为∠AOB的角平分线,请你评判这种作法的正确性并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①.AD=BC;②.DE=CF;③.BE∥AF.
⑴.请用其中两个关系式作为条件,另一个作为结论,写出所有正确的结论.
⑵.选择(1)中你写出的一个正确结论,说明它正确的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC; ②∠BCE+∠BCD=180°; ③AF2=EC2﹣EF2; ④BA+BC=2BF.其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,求当他们离目的地还有20千米时,汽车一共行驶的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com