
 如图,A(4,0),B(0,4),直线y=$\frac{1}{3}$x与直线AB交于点C.
如图,A(4,0),B(0,4),直线y=$\frac{1}{3}$x与直线AB交于点C.分析 (1)设直线AB的解析式为y=kx+b(k≠0),根据点A、B的坐标即可求出直线AB的解析式,联立直线AB、OC的解析式成方程组,解方程组即可求出交点C的坐标;
(2)①过点C作CE⊥x轴于点E,过点P作PF⊥OC于点F,由A、B点的坐标即可得出∠ABO=45°,由∠PCO=3∠ABO即可得出∠PCO=135°,∠PCF=45°,根据∠COE的正切即可得出$\frac{CE}{OE}=\frac{PF}{OF}$,由此可求出PF的长,再根据勾股定理即可得出OP的长,进而得出点P的坐标,根据点P、B的坐标即可利用待定系数法求出直线PB的解析式;②由①中OP的长即可得出点P的坐标.
解答 解:(1)设直线AB的解析式为y=kx+b(k≠0),
则有$\left\{\begin{array}{l}{4k+b=0}\\{b=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
∴直线AB的解析式为y=-x+4.
联立直线AB、OC的解析式得:$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{1}{3}x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴点C的坐标为(3,1).
(2)①如图所示,过点C作CE⊥x轴于点E,过点P作PF⊥OC于点F,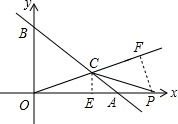
∵A(4,0),B(0,4),
∴∠ABO=45°,
∵∠PCO=3∠ABO,
∴∠PCO=135°,∠PCF=45°,
∵PF⊥OC,
∴PF=CF.
∵C(3,1),
∴CE=1,OE=3,OC=$\sqrt{C{E}^{2}+O{E}^{2}}$=$\sqrt{10}$,
∴tan∠COE=$\frac{CE}{OE}=\frac{PF}{OF}$=$\frac{PF}{\sqrt{10}+PF}$=$\frac{1}{3}$,
∴PF=$\frac{\sqrt{10}}{2}$,OF=$\frac{3\sqrt{10}}{2}$,
∴OP=$\sqrt{P{F}^{2}+O{F}^{2}}$=5,
∴P(5,0).
设直线PB的解析式为y=mx+n(m≠0),
则有$\left\{\begin{array}{l}{n=4}\\{5m+n=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-\frac{4}{5}}\\{n=4}\end{array}\right.$,
∴直线PB的解析式为y=-$\frac{4}{5}$x+4.
②由①可得知:点P的坐标为(5,0).
点评 本题考查了待定系数法求函数解析式、勾股定理以及解直角三角形,解题的关键是:(1)联立直线AB、OC的解析式成方程组;(2)①利用待定系数法求出直线PB的解析式;②求OP的长.本题属于中档题,难度不大,解决该题型题目时,通过解直角三角形中的角的正切值找出边的比例关系是关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-3,2) | C. | (2,-3) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 90 | 90 |
| 面试 | 100 | 70 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,且点C的横坐标是6,连接CA并延长交y轴于点P,连接BP,BC.则△PBC的面积是24.
如图,在平面直角坐标系xOy中,直线y=$\frac{3}{2}$x与双曲线y=$\frac{6}{x}$相交于A,B两点,C是第一象限内双曲线上一点,且点C的横坐标是6,连接CA并延长交y轴于点P,连接BP,BC.则△PBC的面积是24.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李东东在一次钓鱼比赛中,荣获冠军,如图是他根据钓获的鱼的情况绘制的频数分布直方图,根据图示回答下列问题:
李东东在一次钓鱼比赛中,荣获冠军,如图是他根据钓获的鱼的情况绘制的频数分布直方图,根据图示回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
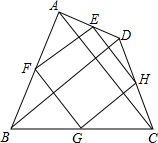 四边形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点
四边形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com