
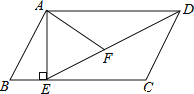
【题目】如图,在平行四边形ABCD中,过点A作AE垂直BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
【答案】(1)证明见解析;(2)6
【解析】试题分析:(1)利用平行四边形的性质得出∠ADF=∠DEC,利用等角的补交相等得出∠AFD=∠C,所以△ADF∽△DEC;(2)根据相似三角形的性质得出DE的长,利用勾股定理得出AE的长.
试题解析:(1)∵四边形ABCD是平行四变形,
∴AB∥CD,AD∥BC,∴∠C+∠B=180°,∠ADF=∠DEC.∵∠AFD+∠AFE=180°,
∠AFE=∠B,∴∠AFD=∠C.在△ADF与△DEC中,
![]()
∴△ADF∽△DEC.
(2)由(1)知△ADF∽△DEC,则:∵四边形ABCD是平行四边形,
![]() ∴CD=AB=8.∴DE=12,在Rt△ADE中,由勾股定理得:AE=
∴CD=AB=8.∴DE=12,在Rt△ADE中,由勾股定理得:AE=![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算。
(1)5﹣(﹣6)+(﹣8)
(2)(﹣ ![]() )﹣0.125﹣(﹣0.4)+
)﹣0.125﹣(﹣0.4)+ ![]()
(3)( ![]() ﹣
﹣ ![]() +
+ ![]() )÷(﹣
)÷(﹣ ![]() )
)
(4)﹣12﹣ ![]() ×[(﹣2)3+(﹣3)2].
×[(﹣2)3+(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)计算:6÷(﹣ ![]() +
+ ![]() ). 方方同学的计算过程如下:原式=6÷(﹣
). 方方同学的计算过程如下:原式=6÷(﹣ ![]() )+6÷
)+6÷ ![]() =﹣12+18=6.
=﹣12+18=6.
请你判断方方同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考黑板中老师的讲解,用运算律简便计算(请写出具体的解题过程): ①999×(﹣15);②999× ![]() +333×(﹣
+333×(﹣ ![]() )﹣999×18
)﹣999×18 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.正多边形每个内角都相等;B.正多边形都是轴对称图形;
C.正多边形都是中心对称图形;D.正多边形的中心到各边的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.﹣a(a﹣b)=﹣a2﹣ab
B.(2ab)2÷a2b=4ab
C.2ab3a=6a2b
D.(a﹣1)(1﹣a)=a2﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com