
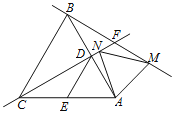
【题目】如图,等边△ABC中,边长为6,D、E分别是AB、AC的中点,连接DE,将△ADE绕点A顺时针旋转得到△AMN,其中D、E的对应点分别是M、N,直线BM与直线CN交于点F,若旋转360°,则点F经过的路径长是( )
A.![]() B.8
B.8![]() C.
C.![]() D.4
D.4![]()
【答案】A
【解析】
设AB交CF于K.首先证明点F在弧![]() 上运动,∠GOK=120°,当旋转360°,则点F经过的路径长是
上运动,∠GOK=120°,当旋转360°,则点F经过的路径长是![]() 的两倍,求出
的两倍,求出![]() 的长度,即可求得答案.
的长度,即可求得答案.
如图,设AB交CF于K.

∵D、E分别是AB、AC的中点,
∴![]() (三角形中位线定理),
(三角形中位线定理),![]() ,
,![]() ,
,
∵△ABC是等边三角形,
∴![]() ,
,
∴△ADE是等边三角形,
由旋转得:![]() ,
,
∴∠CAB=∠MAN=60°,AB=AC,AM=AN,
∴∠CAN=∠BAM,
∴△CAN≌△BAM(SAS),
∴∠ACN=∠ABM,
∵∠CKA=∠BKF,
∴∠BFK=∠CAK=60°,
∵∠CFB=∠CAB=60°,
∴C,B,F,A四点共圆,设圆心为O,
则点F在弧![]() 上运动,∠GOK=120°,
上运动,∠GOK=120°,
∵等边△ABC的边长为6,
∵E是AC的中点,
∴![]() ,
,![]() ,
,
连接OA,则![]() ,
,
设圆的半径为r,

则![]() 的长为:
的长为:![]() ,
,
当旋转360°,则点F经过的路径长是![]() 的两倍,
的两倍,
∴点F经过的路径长=2×![]() =
=![]() π,
π,
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形"ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点C沿着某条路径运动,以点C为旋转中心,将点A(0,4)逆时针旋转90°到点B(m,1),若﹣5≤m≤5,则点C运动的路径长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元.如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,A(2,1),B(3,﹣1),C(﹣2,1),D(0,2).已知线段AB绕着点P逆时针旋转得到线段CD,其中C是点A的对应点.

(1)用尺规作图的方法确定旋转中心P,并直接写出点P的坐标;(要求保留作图痕迹,不写作法)
(2)若以P为圆心的圆与直线CD相切,求⊙P的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
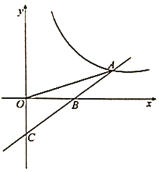
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(1)求k的值;
(2)点P在反比例函数y=![]() (x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
(x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
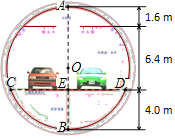
【题目】如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com