方程组$\left\{\begin{array}{l}{x+2y=5}\\{x-y=8}\end{array}\right.$的解也是方程3mx+2my=57的解.求m的值．题目和参考答案——青夏教育精英家教网—

12．方程组$\left\{\begin{array}{l}{x+2y=5}\\{x-y=8}\end{array}\right.$的解也是方程3mx+2my=57的解，求m的值．

分析先解方程组$\left\{\begin{array}{l}{x+2y=5}\\{x-y=8}\end{array}\right.$得$\left\{\begin{array}{l}{x=7}\\{y=-1}\end{array}\right.$，然后把$\left\{\begin{array}{l}{x=7}\\{y=-1}\end{array}\right.$代入方程3mx+2my=57得21m-2m=57，再解关于m的一次方程即可．

解答解：解方程组$\left\{\begin{array}{l}{x+2y=5}\\{x-y=8}\end{array}\right.$得$\left\{\begin{array}{l}{x=7}\\{y=-1}\end{array}\right.$，
把$\left\{\begin{array}{l}{x=7}\\{y=-1}\end{array}\right.$代入方程3mx+2my=57得21m-2m=57，解得m=3．

点评本题考查了二元一次方程组的解：二元一次方程组的两个方程的公共解，叫做二元一次方程组的解．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

9．

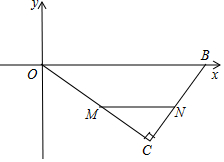已知：如图所示，在平面直角坐标系xOy中，∠C=90°，OB=25，OC=20，若点M是边OC上的一个动点（与点O、C不重合），过点M作MN∥OB交BC于点N．
（1）求点C的坐标；
（2）当△MCN的周长与四边形OMNB的周长相等时，求CM的长；
（3）在OB上是否存在点Q，使得△MNQ为等腰直角三角形？若存在，请求出此时MN的长；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

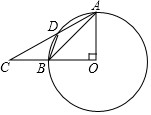如图，∠AOB=90°，C在OB的延长线上，D为⊙O上一点，∠BAD=∠BDC．
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为1，且OB=BC．，求四边形AOBD的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．计算：
（1）（$\sqrt{3}$+$\sqrt{5}$）（$\sqrt{3}$-$\sqrt{5}$）
（2）$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

7．阅读材料：写出二元一次方程x-3y=6的几个解：$\left\{\begin{array}{l}x=0\\ y=-2\end{array}\right.，\left\{\begin{array}{l}x=3\\ y=-1\end{array}\right.，\left\{\begin{array}{l}x=6\\ y=0\end{array}\right.，…$，发现这些解的一般形式可表示为$\left\{\begin{array}{l}x=3m\\ y=m-2\end{array}\right.$（m为有理数）．把一般形式再变形为$\left\{\begin{array}{l}m=\frac{x}{3}\\ m=y+2\end{array}\right.$，可得$\frac{x}{3}=y+2$，整理得原方程x-3y=6．
根据阅读材料解答下列问题：若二元一次方程x+by=c的解，可以写成$\left\{\begin{array}{l}x=2n\\ y=n+1\end{array}\right.$（n为有理数），则1+b+c=-3．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

17．如果关于x的不等式（a+b）x+2a-b＞0的解集是x＜$\frac{5}{2}$，那么关于x的不等式（b-a）x+a+2b≤0的解集是x≥-$\frac{5}{4}$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

4．某班共有60人参加杜会实践拾棉花劳动，某天，这个班学生拾棉花的数量都在30kg以上，拾棉花的数量具体分组如表所示：