练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．设a，b是方程x2+2x-2019=0的两个不相等的实数根．
    （1）a+b=-2；ab=-2019；2a2+4a=4038；
    （2）求代数式a2+3a+b的值．

    分析 （1）直接利用根与系数的关系可得a+b；ab，利用方程的解的定义得出a2+2a=2019进而求出2a2+4a即可；
    （2）a2+3a+b变形为a2+2a+a+b，利用（1）的a2+2a=2019可得结果．

    解答 解：由根与系数的关系得：
    a+b=-2，ab=-2019，
    ∵a是方程x2+2x-2019=0的实数根，
    ∴a2+2a=2019，
    ∴2a2+4a=2×2019=4038；
    故答案为：-2，-2019，4038；

    （2）a2+3a+b=a2+2a+a+b
    =2019-2
    =2017．

    点评 此题主要考查了根与系数的关系以及方程的解，得出a，b的关系是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．将背面相同，正面分别标有数字1、2、3、4的四张卡片洗匀后，背面朝上放在桌子上．请用树状图或列表法解答下列问题：
    （1）从中随机抽取两张卡片，求卡片正面上的数字之积大于4的概率；
    （2）若先从中随机抽取一张卡片（不放回），将该卡片正面上的数字作为十位上的数字；再随机抽取一张，将该卡片正面上的数字作为个位上的数字，求组成的两位数恰好是3的倍数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．某公司需要从甲、乙两个仓库向A、B两地分别运送100t和50t的物资．已知该物资在甲仓库有80t，乙仓库有70t．从甲、乙两个仓库运送物资到A、B两地的运费如下表：
    目的地运费/（元/t）
    甲仓库乙仓库
    A地140200
    B地10080
    （1）设从甲仓库运送到A地的物资为xt，求运送的总运费y（单位：元）与x（单位：t）之间的函数解析式，并写出x的取值范围．
    （2）请你设计出运费最低的运送方案，并求出最低运费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解方程组：$\left\{\begin{array}{l}{{x}^{2}+4xy+4y=1}\\{{x}^{2}+xy=0}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

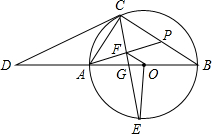    4．如图，AB为⊙O的直径，CD切⊙O于点C，与BA的延长线交于点D，OE⊥AB交⊙O于点E，连接CA、CE、CB，CE交AB于点G，过点A作AF⊥CE于点F，延长AF交BC于点P．
    （Ⅰ）求∠CPA的度数；
    （Ⅱ）连接OF，若AC=$\sqrt{3}$，∠D=30°，求线段OF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

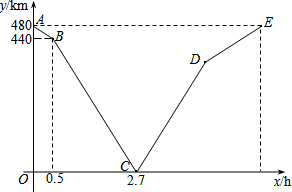    14．一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设一辆车先出发xh后，另一辆车也开始行驶，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系．根据图象解决以下问题：
    （1）慢车的速度为80km/h，快车的速度为120km/h；
    （2）求线段CD的函数解析式，并写出自变量x的取值范围；
    （3）求当x为多少时，两车之间的距离为300km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．若a+b=3，则代数式（$\frac{{b}^{2}}{a}$-a）÷$\frac{a-b}{a}$的值为（　　）
    A．3B．-3C．$\frac{1}{3}$D．-$\frac{1}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

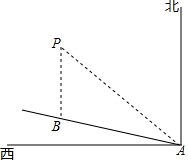    18．如图，一艘船以每小时24海里的速度向北偏西75°方向航行，在点A处测得灯塔P在船的西北方向，航行40分钟后到达点B处，这时灯塔P恰好在船的正北方向，已知距离灯塔9海里以外的海区为安全航行区域，问这艘船能否按原方向继续向前航行？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

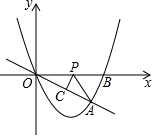    19．如图，在平面直角坐标系中，直线OA与抛物线y=ax2+bx交于原点O和点A（4，-2），点B（5，0）在抛物线上，点P是x轴上一动点，PC⊥OA于点C，连接PA．
    （1）求直线OA的关系式及a、b的值；
    （2）①点P运动到何位置时，PO=PC，求出此时点P的坐标
             ②点P运动到何位置时，若PA+PC存在最小值，求此最小值．
    （3）点M是抛物线上一点，过点MN⊥y轴于点N，若△MON与△AOB相似，请直接写出所有满足条件的点M的坐标．

    查看答案和解析>>

    同步练习册答案