
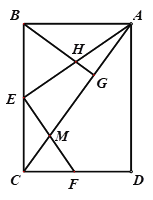
【题目】 如图,![]() 是矩形
是矩形![]() 的边
的边![]() 上的一点,AC是其对角线,连接AE,过点E作
上的一点,AC是其对角线,连接AE,过点E作![]() 交
交![]() 于点
于点![]() ,
, ![]() 交DC于点F,过点B作
交DC于点F,过点B作![]() 于点G,
于点G,![]() 交AE于点H.
交AE于点H.
(1)求证:![]() ∽
∽![]() ;
;
(2)求证:![]() ;
;
(3)若E是BC的中点,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)先利用等角的余角相等证明∠BAE=∠CEF,进一步即可证得结论;
(2)先利用等角的余角相等证明∠ABG=∠ACB,进而可证明△ABH∽△ECM,再利用相似三角形的性质即可证得结论;
(3)由(1)利用相似三角形的性质可求出CF的长,进而利用勾股定理可求出EF的长,延长FE交AB的延长线于点N,易证△NBE≌△FCE,于是NB=FC,NE=FE,由CF∥AN可得△CMF∽△AMN,然后利用相似三角形的性质可求出FM的长,进一步即可求出结果.
解:(1)证明:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,
∴∠BAE+∠AEB=90°,
∵![]() ,∴∠AEB+∠CEF=90°,
,∴∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∴![]() ∽
∽![]() ;
;
(2)证明:∵![]() ,∴∠BAG+∠ABG=90°,
,∴∠BAG+∠ABG=90°,
又∵∠BAC+∠ACB=90°,∴∠ABG=∠ACB,
∵∠BAH=∠ECM,
∴△ABH∽△ECM,
∴![]() ,
,
即![]() ;
;
(3)∵![]() ,
,![]() ,∴BC=8,∵E是BC的中点,∴BE=CE=4,
,∴BC=8,∵E是BC的中点,∴BE=CE=4,
由(1)知![]() ∽
∽![]() ,则
,则![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
则在Rt△CEF中,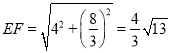 ,
,
延长FE交AB的延长线于点N,
∵∠NBE=∠FCE=90°,BE=CE,∠NEB=∠FEC,
∴△NBE≌△FCE,∴NB=FC,NE=FE,
∵CF∥AN,∴△CMF∽△AMN,∴ ,
,
∴![]() ,
,
∴![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图是一张长12dm,宽6dm的长方形纸板,将纸板四个角各剪去一个同样的边长为xdm的正方形,然后将四周突出部分折起,可制成一个无盖长方体纸盒.
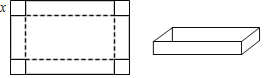
(1)无盖方盒盒底的长为 dm,宽为 dm(用含x的式子表示).
(2)若要制作一个底面积是40dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
(1)当t=2时,点D的坐标是 ;
(2)请用含t的代数式表示出点D的坐标 ;
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
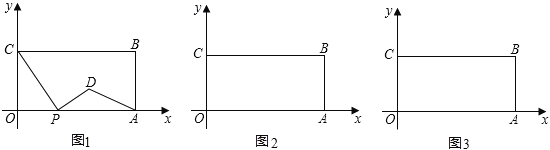
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点C,D分别在反比例函数y=![]() (x>0).y=
(x>0).y=![]() (x>0)的图象上,顶点A,B在x轴上,连接OC,交DA于点E,则
(x>0)的图象上,顶点A,B在x轴上,连接OC,交DA于点E,则![]() =_____.
=_____.
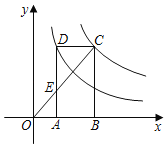
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
| 0 | 2 | 3 | 4 |
| 5 | 0 |
|
| 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④3是方程
;④3是方程![]() 的一个根;⑤若
的一个根;⑤若![]() ,
,![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点C(O,4),与
轴交于点C(O,4),与![]() 轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴
轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴![]() 与抛物线交于点D,与直线BC交于点E.
与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线Z与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。
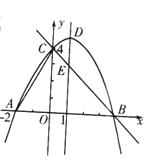
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在圆上,连接AE,AE与BD相交于点F.
(1)求证:AE=AB;
(2)若E为弧BD的中点,试说明:DE2=EF·AE;
(3)在(2)的条件下,若cos∠ADB=![]() ,BE=2,求AF的长.
,BE=2,求AF的长.
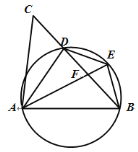
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com