
【题目】已知⊙O的半径为3,A为圆内一定点,AO=1,P为圆上一动点,以AP为边作等腰△APQ,AP=PQ,∠APQ=120°,则OQ的最大值为( )
A.1+3![]() B.1+2
B.1+2![]() C.3+
C.3+![]() D.3
D.3![]()
【答案】A
【解析】
以点P为顶点作等腰三角形OPM,OP=PM,可以证明△AOP≌△QMP,可得MQ=OA=1,作![]() 于
于![]() ,根据三角函数可得OM=
,根据三角函数可得OM=![]()
![]() ,根据三角形三边关系可得OQ≤OM+MQ=
,根据三角形三边关系可得OQ≤OM+MQ=![]() +1,当且仅当M在OQ上时,取等号,即可得结论.
+1,当且仅当M在OQ上时,取等号,即可得结论.
解:如图,
![]()

以点P为顶点作等腰三角形OPM,OP=PM,
∠OPM=120,
∵∠APQ=120°,
∴∠OPM=∠APQ,
∵∠OPA+∠APM=∠MPQ+∠APM,
∴∠OPA=∠MPQ,
∵AP=PQ,OM=PM,
∴△AOP≌△QMP(SAS),
∴MQ=OA=1,
如图,在![]() 中,作
中,作![]() 于
于![]() ,
,
![]()
![]()

![]()
![]() ∠POM=30°,
∠POM=30°,
∴OH=OPcos30°=![]()
![]()
∴OQ≤OM+MQ=![]()
当且仅当M在OQ上时,取等号,
则OQ的最大值为![]()
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线![]() 与x轴,y轴分别交于点A,B,点
与x轴,y轴分别交于点A,B,点![]() 在第一象限内,连结
在第一象限内,连结![]() ,
,![]() ,
,![]() .动点P在
.动点P在![]() 上从点A向终点B匀速运动,同时,动点Q在
上从点A向终点B匀速运动,同时,动点Q在![]() 上从点C向终点O匀速运动,它们同时到达终点,连结
上从点C向终点O匀速运动,它们同时到达终点,连结![]() 交
交![]() 于点D.
于点D.
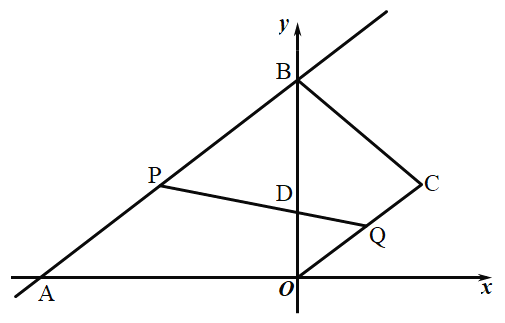
(1)求点B的坐标和a的值;
(2)当点Q运动到![]() 中点时,连结
中点时,连结![]() ,求
,求![]() 的面积;
的面积;
(3)作![]() 交直线
交直线![]() 于点R.
于点R.
①当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长度;
的长度;
②记![]() 交
交![]() 于点E,连结
于点E,连结![]() ,则
,则![]() 的最小值为__________.(直接写出答案)
的最小值为__________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于(﹣1,0),(3,0)两点,则下列判断中,错误的是( )

A.图象的对称轴是直线x=1
B.当﹣1<x<3时,y<0
C.当x>1时,y随x的增大而减小
D.一元二次方程中ax2+bx+c=0的两个根是﹣1和3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
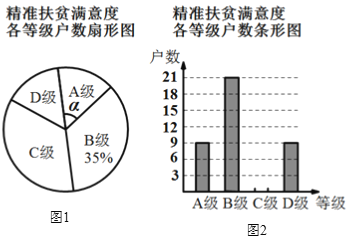
(1)本次抽样调查测试的建档立卡贫困户的总户数______.
(2)图1中,∠α的度数是______,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为![]() )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户
)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.∠ABC的平分线交AC于点O,以点O为圆心,OC为半径.在△ABC同侧作半圆O.
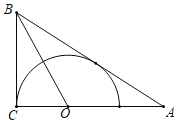
(1)求证:AB与⊙O相切;
(2)若AB=5,AC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtABC中,∠ACB=90°,以AC为直径的⊙O与边AB交于点D,过点D作⊙O的切线,交BC于E.

(1)求证:点E是边BC的中点;
(2)求证:BC2=BDBA;
(3)当AC=BC时,四边形OCED是什么四边形,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
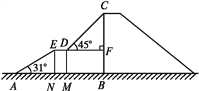
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com