
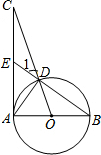
 如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.
如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.分析 (1)由AB为⊙O的直径,AC为⊙O的切线,易证得∠CAD=∠BDO,继而证得结论;
(2)由(1)易证得△CAD∽△CDE,然后由相似三角形的对应边成比例,求得CD的长,再利用勾股定理,求得答案.
解答 (1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
∵AC为⊙O的切线,
∴OA⊥AC,
∴∠OAD+∠CAD=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠1=∠BDO,
∴∠1=∠CAD;
(2)解:∵∠1=∠CAD,∠C=∠C,
∴△CAD∽△CDE,
∴CD:CA=CE:CD,
∴CD2=CA•CE,
∵AE=EC=2,
∴AC=AE+EC=4,
∴CD=2$\sqrt{2}$,
设⊙O的半径为x,则OA=OD=x,
则Rt△AOC中,OA2+AC2=OC2,
∴x2+42=(2$\sqrt{2}$+x)2,
解得:x=$\sqrt{2}$.
∴⊙O的半径为$\sqrt{2}$.
点评 此题考查了切线的性质、圆周角定理以及相似三角形的判定与性质.注意证得△CAD∽△CDE是解此题的关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.89×102 | B. | 389×102 | C. | 3.89×104 | D. | 3.89×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
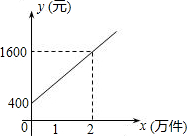 某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=3}\\{x-y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=-1}\\{x-y=-3}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com