



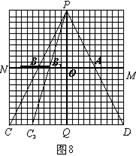
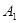 A∽△PD
A∽△PD D,
D, ,
, ,∴D1D
,∴D1D
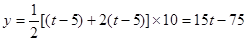
 ………………4分
………………4分
 C2D2,且A2B2=5
C2D2,且A2B2=5 ∴
∴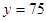 …………6分
…………6分

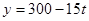 ………………………………8分
………………………………8分 的性质可知,盲区的面积由0逐渐增大到75;
的性质可知,盲区的面积由0逐渐增大到75;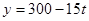 的性质可知,盲区的面积由75逐渐减小到0
的性质可知,盲区的面积由75逐渐减小到0 ………………………………………………9分
………………………………………………9分

科目:初中数学 来源:不详 题型:解答题
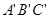 是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
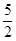 ,3),则A′的坐标为 ;
,3),则A′的坐标为 ;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 ,CH=2,求BC的长.
,CH=2,求BC的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
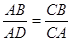 中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】
中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】 
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x
AB=12.动点P、Q分别在边AD和BC上,且BQ=3DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x
 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛
C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛 物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com