Question

20．如图1，在Rt△AOC中，∠ACO=90°，动点P从点A出发以每秒1个单位的速度沿AO向终点O运动，动点Q从点O出发以每秒2个单位的速度沿y轴正半轴运动，连接PQ，若P，Q两点同时出发，当点P到达终点时点Q也停止运动，过点D作PD⊥AO交y轴正半轴于点D，设动点P运动的时间为t秒，图2是△PDQ的面积S与运动时间t的完整图象，BE，EF为曲线，且B（0，$\frac{50}{3}$），F（5，0）

（1）求△PDQ的面积S关于t的函数关系式；
（2）是否存在某一时刻t，使△PDQ为等腰三角形，若存在，求出点Q的坐标，若不存在，请说明理由．
（3）过点P作PG⊥OC于点G，连接DG，把△PDG沿直线PD折叠，当点G的对应点G′恰好落在AC边上时，请求出t的值．

Answer 1

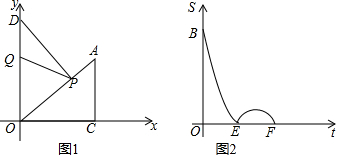
分析 （1）如图1中，作AM⊥OA于M．由题意OA=5，$\frac{1}{2}$•OA•AM=$\frac{50}{3}$，推出AM=$\frac{20}{3}$，OM=$\sqrt{O{A}^{2}+A{M}^{2}}$=$\sqrt{{5}^{2}+（\frac{20}{3}）^{2}}$=$\frac{25}{3}$，由△OAM∽△ACO，推出$\frac{OA}{AC}$=$\frac{AM}{CO}$=$\frac{OM}{OA}$，求出DP，OD，分两种情形讨论即可．
（2）分三种情形讨论0≤t≤$\frac{25}{11}$时，①当DQ=PD时，②当PQ=PD时，cos∠PDQ=$\frac{\frac{1}{2}[\frac{5}{3}（5-t）-2t]}{\frac{4}{3}（5-t）}$=$\frac{4}{5}$，③当QD=QP时，cos∠PDQ=$\frac{\frac{1}{2}•\frac{4}{3}（5-t）}{\frac{5}{3}（5-t）-2t}$=$\frac{4}{5}$，$\frac{25}{11}$＜t≤5时，只有DQ=DP时，△DPQ是等腰三角形，列出方程解方程即可．
（3）由PG∥AC，推出$\frac{PG}{AC}$=$\frac{OP}{OA}$，即$\frac{PG}{3}$=$\frac{5-t}{5}$，推出PG=PG′=$\frac{3}{5}$（5-t），由∠OPG=∠APG′=∠AOC，推出PG′=AG′=PG，根据$\frac{\frac{1}{2}AP}{AG′}$=cos∠OAC=$\frac{3}{5}$，列出方程即可解决问题．

解答 解：（1）如图1中，作AM⊥OA于M．

由题意OA=5，$\frac{1}{2}$•OA•AM=$\frac{50}{3}$，
∴AM=$\frac{20}{3}$，OM=$\sqrt{O{A}^{2}+A{M}^{2}}$=$\sqrt{{5}^{2}+（\frac{20}{3}）^{2}}$=$\frac{25}{3}$
∵AC∥OD，
∴∠AOM=∠OAC，∠OAM=∠ACO=90°，
∴△OAM∽△ACO，
∴$\frac{OA}{AC}$=$\frac{AM}{CO}$=$\frac{OM}{OA}$，
∴$\frac{5}{AC}$=$\frac{\frac{20}{3}}{OC}$=$\frac{\frac{25}{3}}{5}$，
∴AC=3，OC=4，
由△OPD∽△ACO，得$\frac{OP}{AC}$=$\frac{PD}{CO}$=$\frac{OD}{AO}$，
∴$\frac{5-t}{3}$=$\frac{PD}{4}$=$\frac{OD}{5}$，
∴OD=$\frac{5}{3}$（5-t），PD=$\frac{4}{3}$（5-t），
当OQ=OD时，2t=$\frac{5}{3}$（5-t），解得t=$\frac{25}{11}$，
①当0≤t≤$\frac{25}{11}$时，作PH⊥OD于H．易知PH=$\frac{4}{5}$（5-t），
∴S=$\frac{1}{2}$•DQ•PH=$\frac{1}{2}$•[$\frac{5}{3}$（5-t）-2t]•$\frac{4}{5}$（5-t）=$\frac{22}{15}$t²-12t+10．

②当$\frac{25}{11}$＜t≤5时，如图2中，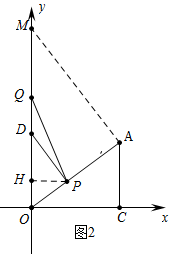

S=$\frac{1}{2}$DQ•PH=-$\frac{22}{15}$t²+12t-10．
综上所述，S=$\left\{\begin{array}{l}{\frac{22}{15}{t}^{2}-12t+10}&{（0≤t≤\frac{25}{11}）}\\{-\frac{22}{15}{t}^{2}+12t-10}&{（\frac{25}{11}＜t≤5）}\end{array}\right.$．

（2）0≤t≤$\frac{25}{11}$时，①当DQ=PD时，$\frac{5}{3}$（5-t）-2t=$\frac{4}{3}$（5-t），解得t=$\frac{5}{7}$．

②当PQ=PD时，cos∠PDQ=$\frac{\frac{1}{2}[\frac{5}{3}（5-t）-2t]}{\frac{4}{3}（5-t）}$=$\frac{4}{5}$，解得t=$\frac{35}{23}$．

③当QD=QP时，cos∠PDQ=$\frac{\frac{1}{2}•\frac{4}{3}（5-t）}{\frac{5}{3}（5-t）-2t}$=$\frac{4}{5}$，解得t=$\frac{25}{17}$．
$\frac{25}{11}$＜t≤5时，只有DQ=DP时，△DPQ是等腰三角形，2t-$\frac{5}{3}$（5-t）=$\frac{4}{3}$（5-t），解得t=3．
综上所述，t=$\frac{5}{7}$s或$\frac{35}{23}$s或$\frac{25}{17}$s或3s时，△PDQ是等腰三角形．

（3）如图3中，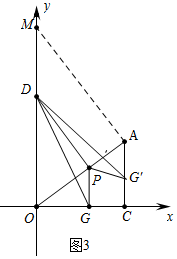

∵PG∥AC，
∴$\frac{PG}{AC}$=$\frac{OP}{OA}$，
∴$\frac{PG}{3}$=$\frac{5-t}{5}$，
∴PG=PG′=$\frac{3}{5}$（5-t），
∵∠OPG=∠APG′=∠AOC，
∴PG′=AG′=PG，
∵$\frac{\frac{1}{2}AP}{AG′}$=cos∠OAC，
∴$\frac{\frac{1}{2}t}{\frac{3}{5}（5-t）}$=$\frac{3}{5}$，
∴t=$\frac{90}{43}$，
∴t=$\frac{90}{43}$s时，点G的对应点G′恰好落在AC边上．

点评 本题考查三角形综合题、相似三角形的判定和性质、翻折变换、平行线分线段成比例定理、等腰三角形的判定和性质、锐角三角函数等知识，解题的关键是学会分类讨论，学会用方程的思想思考问题，属于中考压轴题．