
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x=![]() .
.

(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
科目:初中数学 来源: 题型:
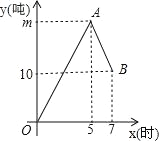
【题目】某仓库有甲、乙、丙三辆运货车,在满载的情况下,甲车每小时可运货6吨,乙车每小时可运货10吨,某天只有乙车负责进货,甲车和丙车负责出货.如图是从早晨上班开始库存量y(吨)与时间x(时)之间的函数图象,OA段表示甲、乙两车一起工作,AB段表示乙、丙两车一起工作,且在工作期间,每辆车都是满载的.
(1)m= .
(2)在满载的情况下,丙车每小时可运货 吨.
(3)求AB段中库存量y(吨)与时间x(时)之间的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式能用平方差公式计算的是( )
A. (3a+b)(a﹣b) B. (3a+b)(﹣3a﹣b) C. (﹣3a﹣b)(﹣3a+b) D. (﹣3a+b)(3a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月5日,十三届全国人大一次会议在人民大会堂开幕,会议听取了国务院总理李克强关于政府工作的报告,其中表示,五年来,人民生活持续改善,脱贫攻坚取得决定性进展,贫困人口减少6800多万,易地扶贫搬迁830万人,贫困发生率由10.2%下降到3.1%,将830万用科学记数法表示为( )
A. 83×105 B. 0.83×106 C. 8.3×106 D. 8.3×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
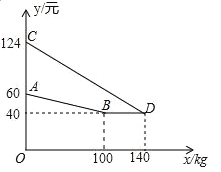
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(﹣3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=![]() x+m从点C开始沿y轴向下平移.
x+m从点C开始沿y轴向下平移.
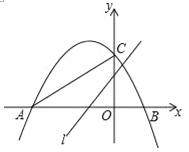
(1)当直线l上点D满足DA=DC且∠ADC=90°时,m的值为 _________ ;
(2)以动直线l为对称轴,线段AC关于直线l的对称线段A′C′与抛物线有交点,写出m的取值范围 _________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com