
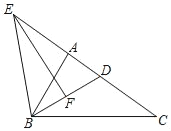
【题目】已知:如图,在△ABC中,点D在边AC上,BD的垂直平分线交CA的延长线于点E,交BD于点F,联结BE,ED2=EAEC.
(1)求证:∠EBA=∠C;
(2)如果BD=CD,求证:AB2=ADAC.
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:已知方程![]() ,求一元二次方程,使它的根分别是已知方程根的2倍.
,求一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为![]() ,则
,则![]() ,所以
,所以![]() .
.
把![]() 代入已知方程,得
代入已知方程,得![]()
化简,得![]()
故所求方程为![]() .
.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: .
,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: .
(2)已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
(3)已知关于![]() 的方程
的方程![]() 有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
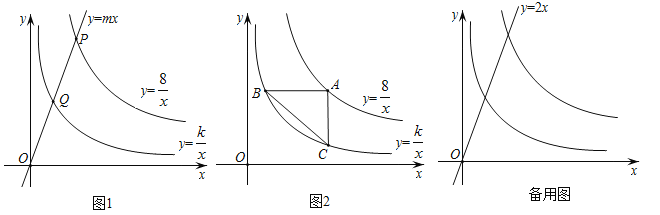
【题目】如图1,已知直线y=mx分别与双曲线y=![]() ,y=
,y=![]() (x>0)交于P,Q两点,且OP=2OQ.
(x>0)交于P,Q两点,且OP=2OQ.
(1)求k的值;
(2)如图2,若A是双曲线y=![]() 上的动点,AB∥x轴,AC∥y轴,分别交双曲线y=
上的动点,AB∥x轴,AC∥y轴,分别交双曲线y=![]() (x>0)于B,C两点,连接BC,设A点的横坐标为t.
(x>0)于B,C两点,连接BC,设A点的横坐标为t.
①分别写出A,B,C的坐标,并求△ABC的面积;
②当m=2时,D为直线y=2x上的一点,若以A,B,C,D为顶点的四边形是平行四边形,求A点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲,乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )
A. ![]() =
=![]() B.
B. ![]() =
=![]()
C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 随着互联网、移动终端的迅速发展,数字化阅读越来越普及. 公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
“您如何看待教化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化间读问调查表,请在表格中选择一项您最认观点,在其后空格内打“√”,非常感谢您的合作.
随着互联网、移动终端的迅速发展,数字化阅读越来越普及. 公交、地铁上的“低头族”越来越多,某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷训查表如下图所示),并将调查结果绘制成图①和图②所示的统计图(均不完整).
“您如何看待教化阅读”问卷调查表
您好!这是一份关于“您如何看待数字化间读”问调查表,请在表格中选择一项您最认观点,在其后空格内打“√”,非常感谢您的合作.
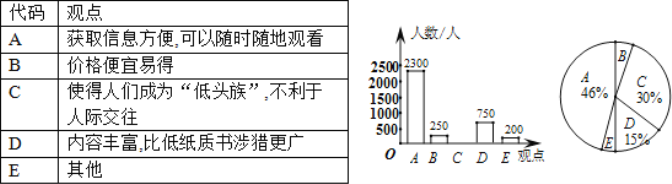
请根据统计图中提供的信息,解答下列问题:
(1)本次接受词查的总人数是______人,并将条形统计图补充完整;
(2)在扇形统计图中,观点E的百分比是_______,表示观点B的扇形的圆心角度数为______度.
(3)某市共有300万人,请根据以上调查结果估算该市持![]() 观点赞成数字化阅读的人数共有多少万人.
观点赞成数字化阅读的人数共有多少万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春晓中学为开展“校园科技节”活动,计划购买A型、B型两种型号的航模.若购买8个A型航模和5个B型航模需用2200元;若购买4个A型航模和6个B型航模需用1520元.求A,B两种型号航模的单价分别是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
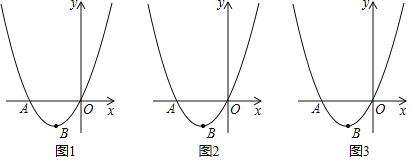
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于点A,顶点B的坐标为(﹣2,﹣2).
(1)求a,b的值;
(2)在y轴正半轴上取点C(0,4),在点A左侧抛物线上有一点P,连接PB交x轴于点D,连接CB交x轴于点F,当CB平分∠DCO时,求点P的坐标;
(3)在(2)的条件下,连接PC,在PB上有一点E,连接EC,若∠ECB=∠PDC,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD内接于⊙O,AB=AC,BD为⊙O的直径,AE⊥BD,垂足为点E,交BC于点F.
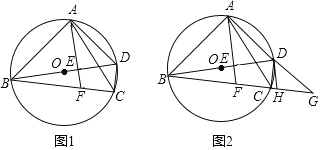
(1)求证:FA=FB;
(2)如图2,分别延长AD,BC交于点G,点H为FG的中点,连接DH,若tan∠ACB=![]() ,求证:DH为⊙O的切线;
,求证:DH为⊙O的切线;
(3)在(2)的条件下,若DA=3![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com