练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．三角形的三个内角比为1：2：3，最小的边长为1，则最大的边长为（　　）
    A．2B．4C．6D．8

    分析 根据三角形内角和定理求出三角形的三个内角的度数，根据直角三角形的性质计算即可．

    解答 解：设三角形的三个内角分别为x、2x、3x，
    由三角形内角和定理得，x+2x+3x=180°，
    解得，x=30°，
    ∴3x=90°，
    ∴最大的边长为1×2=2，
    故选：A．

    点评 本题考查的是直角三角形的性质、三角形内角和定理的应用，掌握直角三角形中，30°角所对的直角边等于斜边的一半是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．解下列不等式（组）：
    （1）2x-$\frac{2x-3}{4}＜\frac{2+5x}{3}$
    （2）$\left\{\begin{array}{l}3-5x＞x-2（2x+3）\\ 3x+5＞x-7\end{array}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

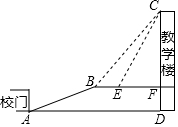    16．某山区为改善办学条件，依山新建一座教学楼，校门A处，有一坡度i=5：12的斜坡AB，在坡顶B处（铅直高度为10米）看教学楼CF的楼顶C的仰角∠CBF=53°，在E处仰角C的仰角∠CEF=63.4°，按规划要在离B点6米远的E处建一悬挂国旗的旗杆．
    （1）求斜坡AB的长度；
    （2）求旗杆处离教学楼的距离．
    （参考数据：tan63.4°≈2，tan53°≈$\frac{4}{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：
    （1）（a-1）2-a（a-2）；               
    （2）（x-6）（x+4）+（3x+2）（2-3x）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，已知在△ABC中，DE∥CA，∠1=∠2，∠3=∠4，∠BAC=84°．求∠EDA的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

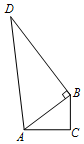    10．某机器零件呈四边形ACBD的形状，要求∠ABD=90°，∠C=90°．现测得∠ABD=90°，AD=39，BD=36，AC=12，BC=9．你认为这个零件合格吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．以下是小明的计算过程，请你仔细观察，错误的步骤是（　　）
    $\sqrt{9}-{（-2）^2}-|{1-\sqrt{2}}|-\root{3}{-8}$
    解：原式=$3-{（-2）^2}-|{1-\sqrt{2}}|-\root{3}{-8}$①
    =$3-4-|{1-\sqrt{2}}|-\root{3}{-8}$②
    =3-4-$\sqrt{2}-1-\root{3}{-8}$③
    =3-4-$\sqrt{2}$-1+2④
    =-$\sqrt{2}$．
    A．①B．②C．③D．④

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1min仰卧起坐次数，并绘制如图所示的频数直方图，请根据图中的信息，计算仰卧起坐次数在25∽30次的百分比是（　　）
    A．40%B．30%C．20%D．10%

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下面的四个点中，有一个不在一次函数y=-2x+1的图象上，这个点是（　　）
    A．（2，-3）B．（-2，3）C．（$\frac{1}{2}$，0）D．（0，1）

    查看答案和解析>>

    同步练习册答案