练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．如图，平行四边形ABCD中，E在CD延长线上，AB=10，DE=5，EF=6，求BF的长．

    分析 由平行四边形的性质得出AB=CD=10，AB∥CD，得出内错角相等∠E=∠ABF，证出AB=AF，得出∠AFB=∠ABF，由对顶角相等得出∠E=∠DFE，得出DE=DF即可

    解答 解：∵四边形ABCD是平行四边形，
    ∴AB∥CD，∴△ABF∽△DEF，
    ∴$\frac{AB}{DE}=\frac{BF}{EF}$，
    ∴BF=$\frac{AB•EF}{DE}=\frac{10×6}{5}=12$
    答：BF的长为12．

    点评 本题考查了平行四边形的性质、相似三角形的判定和性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．试举出一个实例，说明$\frac{400}{x}$-$\frac{400}{x+10}$的实际意义．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．小明与小丽在研究代数式2x2-4x-1和x2-2x-4时发生了争执，小明认为无论x取何值，2x2-4x-1的值总大于x2-2x-4的值；而小丽则认为它们的大小关系随x的变化而变化，你认为谁的判断正确？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．在理解例题的基础上，完成下列两个问题：
    例题：若m2+2mn+2n2-6n+9=0．求m和n的值．
    解：因为m2+2mn+2n2-6n+9=（m2+2mn+n2）+（n2-6n+9）=（m+n）2+（n-3）2=0
    所以m+n=0，n-3=0
    即m=-3．n=3
    问题：
    （1）若x2+2xy+2y2-4y+4=0，求xy的值．
    （2）若a、b、c是△ABC的长，满足a2+b2=10a+8b-41，c是△ABC中最长边的边长，且c为整数，求c的值？
    （3）已知a-b=4，ab+c2-6c+13=0，则a+b+c=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

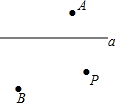    19．如图，平面上有直线a及直线a外的三点A、B、P．
    （1）过点P画一条直线m，使得m∥a；
    （2）过B作BH⊥直线m，并延长BH至B′，使得BB′为直线a、m之间的距离；
    （3）若直线a、m表示一条河的两岸，现要在这条河上建一座桥（桥与河岸垂直），使得从村庄A经桥过河到村庄B的路程最短，试问桥应建在何处？画出示意图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．京东商城销售A、B两种型号的电风扇，销售单价分别为250元、180元，如表是近两周的销售利润情况：
    销售时段销售数量销售利润
    A种型号B种型号
    第一周30台60台3300元
    第二周40台100台5000元
    （进价、售价均保持不变，利润=销售收入-进货成本）
    （1）求A、B两种型号电风扇的每台进价；
    （2）若京东商城准备用不多于5万元的金额采购这两种型号的电风扇共300台，求A种型号的电风扇最多能采购多少台？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．为了让同学们了解自己的体育水平，初二1班的体育康老师对全班45名学生进行了一次体育模拟测试（得分均为整数）成绩满分为10分，成绩达到9分以上（包含9分）为优秀，成绩达到6分以上（包含6分）为合格，1班的体育委员根据这次测试成绩，制作了统计图和分析表如下：

    初二1班体育模拟测试成绩分析表
      平均分 方差 中位数 众数 合格率 优秀率
     男生  2 8 7 95% 40%
     女生 7.92 1.99 8  96% 36%
    根据以上信息，解答下列问题：
    （1）在这次测试中，该班女生得10分的人数为4人，则这个班共有女生25人；
    （2）补全初二1班男生体育模拟测试成绩统计图，并把相应的数据标注在统计图上；
    （3）补全初二1班体育模拟测试成绩分析表；
    （4）你认为在这次体育测试中，1班的男生队、女生队哪个表现更突出一些？并写出一条支持你的看法的理由；
    （5）体育康老师说，从整体看，1班的体育成绩在合格率方面基本达标，但在优秀率方面还不够理想，因此他希望全班同学继续加强体育锻炼，争取在期末考试中，全班的优秀率达到60%，若男生优秀人数再增加6人，则女生优秀人数再增加多少人才能完成康老师提出的目标？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数；用max{a，b，c}表示这三个数中最大的数．
    例如：M{1，2，3}=$\frac{1}{3}$（1+2+3）=2，max{1，2，3}=3，…
    解答下列问题：
    （1）填空：max{-2，-5，-3}=-2；
    （2）如果M{-2，x-1，2x}=max{-2，x-1，2x}，求x的值；
    （3）在同一直角坐标系中作出函数y=x-1，y=-|x+1|，y=-2-x的图象（不需列表描点），通过观察图象，填空：max{x-1，-|x+1|，-2-x}的最小值为-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在Rt△ABC中，∠ABC=90°，点D在边AC上，且∠DBC=∠DCB
    （1）求证：AD=CD；
    （2）若∠A=30°，DE⊥AC，交AB于E，求$\frac{BE}{AE}$的值．

    查看答案和解析>>

    同步练习册答案