
分析 (1)对于直线y=x+4,令x=0求出对应的y值,即为B的纵坐标,确定出B的坐标,得到OB的长,由OC=2OB,求出OC的长,确定出C的坐标,将C的坐标代入直线y=-2x+b中,求出b的值,进而确定出直线CD的解析式;
(2)过P作PG垂直于y轴于G点,连接PQ,由路程=速度×时间,表示出BP与DQ,由一对直角相等,以及一对公共角,利用两对对应角相等的两三角形相似得到三角形BGP与三角形BOC相似,根据OB与OC,利用勾股定理求出BC的长,由相似得比例,将各自的值代入表示出BG和GP,由OB-BG表示出OG,进而表示出P的坐标,同理表示出Q的坐标,由P与Q横坐标相等,得到PQ平行于y轴,可得出d为Q与P纵坐标之差,表示即可,并由d大于0求出t的范围;
(3)由PQ与y轴平行,得到N横坐标与P、Q相同,都为2t,将x=2t代入直线AB解析式中求出对应的y值,即为N的纵坐标,表示出N的坐标,由Q与N的纵坐标之差表示出|NQ|,因为以NQ长为直径的圆与y轴相切,所以|NQ|÷2=2t,解方程即可.
解答 解:(1)对于直线y=x+4,令x=0,
解得:y=4,
故B(0,4),即OB=4,
∴OC=2OB=8,即C(8,0),
将x=8,y=0代入直线y=-2x+b得:0=-16+b,
解得:b=16,
则直线CD的解析式为y=-2x+16;
(2)过点P作PG⊥OB于G点,连接PQ,如图2,
由题意得:BP=$\sqrt{5}$t,DQ=2$\sqrt{5}$t,
由OB=4,OC=8,根据勾股定理得:BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=4$\sqrt{5}$,
∵∠BGP=∠BOC=90°,又∠GBP=∠OBC,
∴△BPG∽△BCO,
∴$\frac{BG}{BO}$=$\frac{GP}{OC}$=$\frac{BP}{BC}$,即$\frac{BG}{4}$=$\frac{GP}{8}$=$\frac{\sqrt{5}t}{4\sqrt{5}}$,
整理得:BG=t,GP=2t,
∴OG=OB-BG=4-t,
∴P(2t,4-t),
同理Q(2t,16-4t)
∴PQ∥y轴,
∴d=PQ=(16-4t)-(4-t)=12-3t(0≤t<4);
(3)由Q(2t,16-4t),PQ∥y轴,
∴N(2t,2t+4),
∴NQ=|12-6t|,
∵以NQ长为直径的圆与y轴相切,
∴2t=$\frac{1}{2}$|12-6t|,
解得:t=$\frac{6}{5}$或6.
点评 此题考查了一次函数与坐标轴的交点,相似三角形的判定与性质,勾股定理,坐标与图形性质,等腰直角三角形的判定与性质,直线与圆的位置关系,利用了转化及分类讨论的数学思想,是一道中考中的常考的压轴题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO=$\frac{1}{2}$,抛物线y=-x2+bx+c过A、B两点.
如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO=$\frac{1}{2}$,抛物线y=-x2+bx+c过A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
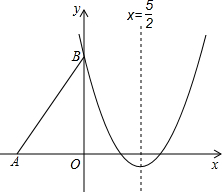 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线y=-$\frac{1}{2}$x+2与坐标轴相交于B、C两点,抛物线也过B、C两点,还与x轴相交于A点,抛物线对称轴与BC相交于E点,顶点为F,∠FEC=∠CAO.
直线y=-$\frac{1}{2}$x+2与坐标轴相交于B、C两点,抛物线也过B、C两点,还与x轴相交于A点,抛物线对称轴与BC相交于E点,顶点为F,∠FEC=∠CAO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(-3,-2).
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(-3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{24000}{x}$=$\frac{24000}{x-400}$+2 | B. | $\frac{24000}{x}$=$\frac{24000}{x-400}$-2 | ||
| C. | $\frac{24000}{x}$=$\frac{24000}{x+400}$-2 | D. | $\frac{24000}{x}$=$\frac{24000}{x+400}$+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,∠BAD=103°-∠2,∠B=77°+∠2,AC⊥CD于F,∠1和∠2相等吗?请把结论或理由填写在下列红线或括号中.
如图,在四边形ABCD中,∠BAD=103°-∠2,∠B=77°+∠2,AC⊥CD于F,∠1和∠2相等吗?请把结论或理由填写在下列红线或括号中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com