
【题目】已知![]() ,点
,点![]() 在
在![]() 上,
上,![]() 垂足为
垂足为![]() ,若
,若![]() 则
则![]() 的面积为____________________.
的面积为____________________.

【答案】![]()
【解析】
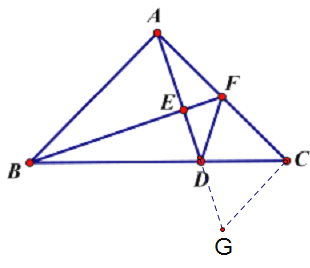
如下图,先证△ABF≌△CAG,得到CG=AF,再证△CDF≌△CDG,得到CF=CG,设EF=x,利用△AEF∽△ACG和△AEF∽△BEA得出ED和DF的长,最后在Rt△EFD中利用勾股定理求得x的值,进而得出△ADF的面积.
如下图,过点C作AC的垂线,交AD的延长线于点G
∵AB=AC,∠BAC=90°
∴△ABC是等腰直角三角形,AB=AC,∠ACB=45°
∵AD⊥BF
∴∠ABE+∠BAE=90°
∵∠DAC+∠BAE=90°,∴∠DAC=∠ABE
在△ABF和△CAG中
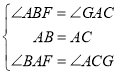
∴△ABF≌△CAG
∴∠AFB=∠AGC,AF=GC
∵∠AFB=∠DFC,∴∠AGC=∠DFC
在△DFC和△DGC中
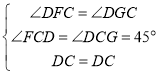
∴△DFC≌△DGC
∴GC=FC
∴AF=FC=![]()
设EF=x
∵∠EAF=∠GAC,∠AEF=∠ACG=90°
∴△AEF∽△ACG
∵AF=FC=GC=![]() ,EF=x
,EF=x
∴![]()
∴AE=2x
同理可证△AEF∽△BEA
∴![]()
∴BE=4x
∴BF=5x=AG
∴DG=AG-AE-ED=5x-2x-2=3x-2=DF
∴在Rt△EFD中,![]()
解得:x=![]()
∴AE=3,EF=![]()
![]()
故答案为:![]()


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
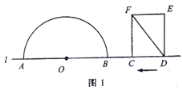
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
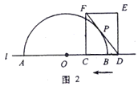
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
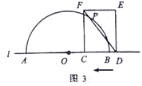
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“防疫有我,爱卫同行”为主题的线上活动,举办了![]() 自制口罩,
自制口罩,![]() 防疫诗歌,
防疫诗歌,![]() 防疫故事,
防疫故事,![]() 防疫画报共四个项目的比赛,要求每位学生必须参加且仅参加一项,小丽随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图,请根据统计图中信息解答下列问题:
防疫画报共四个项目的比赛,要求每位学生必须参加且仅参加一项,小丽随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图,请根据统计图中信息解答下列问题:
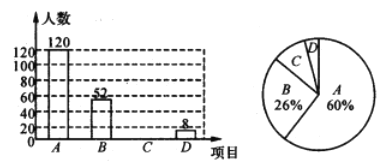
(1)本次调查的学生总人数是多少?扇形统计图中“![]() ”部分的圆心角度数是多少?
”部分的圆心角度数是多少?
(2)请将条形统计图补充完整;
(3)若全校共有1800名学生,请估计该校报名参加防疫故事和防疫画报比赛的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F
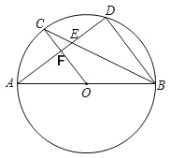
(1)求证:![]() =
=![]() ;
;![]()
(2)若CE=1,EB=3,求⊙O的半径;
(3)若BD=6,AB=10,求D E的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”“10元”“20元”“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出2个小球(第一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用60天的时间销售一种成本为10元每件的商品,经过统计得到此商品的日销售量m(件)、销售单价n(元/件)在第x天(x为正整数)销售的相关信息:
①m与x满足一次函数关系,且第1天的日销售量为98件,第4天的日销售量为92件;
②n与x的函数关系式为:n=![]() .
.
(1)求出第15天的日销售量;
(2)设销售该产品每天利润为y元,请写出y与x的函数关系式,并求出在60天内该产品的最大利润.
(3)在该产品的销售过程中,共有 天销售利润不低于2322元.(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的边长为4,顶点
的边长为4,顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,抛物线
轴上,抛物线![]() 经过点D(-1,0).
经过点D(-1,0).
(1)求点C的坐标;
(2)求抛物线的对称轴;
(3)若抛物线![]() 与正方形
与正方形![]() 的边恰好有三个公共点,求
的边恰好有三个公共点,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com