练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
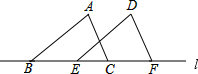
    9．已知△ABC的边在直线l上，BC=5，现把△ABC沿着直线l向右平移到△DEF的位置（如图所示），若EC=3，则△ABC平移的距离为（　　）
    A．2B．3C．5D．7

    分析 求出BE的长度，然后根据平移的性质，对应点连线的长度等于平移距离解答．

    解答 解：∵BC=5，EC=3，
    ∴BE=BC-EC=5-3=2，
    ∵△ABC沿着直线l向右平移到△DEF的位置，
    ∴△ABC平移的距离为BE的长度，
    ∴△ABC平移的距离为2．
    故选A．

    点评 本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等，本题主要利用了平移的距离等于对应点连线的线段长度．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

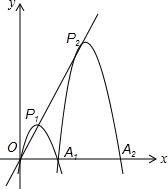    19．已知在平面直角坐标系xOy中，抛物线y1=ax2+bx（a≠0），与x轴正半轴交于点A1（2，0），顶点为P1，△OP1A1为正三角形，现将抛物线y1=ax2+bx（a≠0）沿射线OP1平移，把过点A1时的抛物线记为抛物线y2，记抛物线y2与x轴的另一交点为A2；把抛物线y2继续沿射线OP1平移，把过点A2时的抛物线记为抛物线y3，记抛物线y3与x轴的另一交点为A3；…．；把抛物线y2015继续沿射线OP1平移，把过点A2015时的抛物线记为抛物线y2016，记抛物线y2016与x轴的另一交点为A2016，顶点为P2016．若这2016条抛物线的顶点都在射线OP1上．
    （1）①求△OP1A1的面积；②求a，b的值；
    （2）求抛物线y2的解析式；
    （3）请直接写出点A2016以及点P2016坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．（1）解方程：$\frac{2-x}{x-3}$+$\frac{1}{3-x}$=1
    （2）解不等式组：$\left\{\begin{array}{l}{2（x-2）≤4x-3}\\{2x-5＜1-x}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

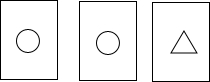    17．小宇手中有15张牌，其中10张牌的背面标记“〇”，5张牌的背面标记“△”，如图是从小宇手中取出的3张牌．若从手中剩余的牌中随机抽出一张牌，每张牌被抽出的机会相等，则抽出标记“○”的牌的概率是$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：$\frac{x^2+1}{x+1}$+$\frac{2x}{x+1}$-x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．反比例函数y=$\frac{m-3}{x}$，在每一象限内，y随x的增大而减小，则m的取值范围m＞3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．观察下列各数：1，1，$\frac{5}{7}$，$\frac{7}{15}$，$\frac{9}{31}$，…按你发现的规律计算这列数的第7个数为（　　）
    A．$\frac{15}{255}$B．$\frac{13}{127}$C．$\frac{11}{127}$D．$\frac{11}{63}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．先化简，再求值：（1-$\frac{x}{{x}^{2}+x}$）÷$\frac{{x}^{2}-1}{{x}^{2}+2x+1}$，其中x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

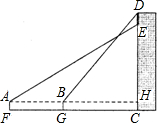    19．如图所示，为了知道楼房CD外墙上一电子屏的高度DE是多少，某数学活动小组利用测角仪和米尺等工具进行如下操作；在A处测得点E的仰角为31°，在B出测得点D的仰角为50°，A、B、H共线，且AH⊥CD于点H，AB为20米，测角仪的高度（AF、BG）为1.6米．已知楼房CD高为34.6米，根据测量数据，请求出DE的高度．（参考数据：tan31°≈0.6，tan50°≈1.2）

    查看答案和解析>>

    同步练习册答案