
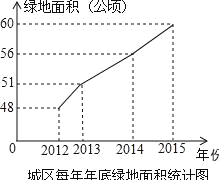
【题目】美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
(1)根据图中所提供的信息回答下列问题:2015年底的绿地面积为 公顷,比2014年底增加了 公顷;在2013年,2014年,2015年这三年中,绿地面积增加最多的是 年;
(2)为满足城市发展的需要,计划到2017年底使城区绿地面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
【答案】(1)60;4;2014;(2)2016,2017两年绿地面积的年平均增长率10%.
【解析】
(1)根据统计图能看出2012年,2013年,2014年,2015年的绿化面积,计算得出每年增加了多少公顷即可解答.
(2)设2016,2017两年绿地面积的年平均增长率为x,根据计划到2017年底使城区绿地面积达到72.6公顷,可列方程求解.
解:(1)根据统计图能看出2012年,2013年,2014年,2015年的绿化面积分别是:48公顷,51公顷,56公顷,60公顷,
60﹣56=4,2015年比2014年底增加了4公顷,
56﹣51=5,2014年比2013年底增加了5公顷,
51﹣48=3,2013年比2012年底增加了3公顷,
这三年中增长最多的是2014年.
答:2015年底的绿地面积为60公顷,比2014年底增加了4公顷;在2013年,2014年,2015年这三年中,绿地面积增加最多的是2014年;
(2)设2016,2017两年绿地面积的年平均增长率为x,
60(1+x)2=72.6.
x=10%或x=﹣210%(舍去).
答:2016,2017两年绿地面积的年平均增长率10%.
故答案为:(1)60;4;2014;(2)2016,2017两年绿地面积的年平均增长率10%.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
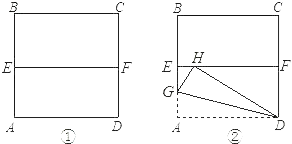
【题目】有一边长为2的正方形纸片ABCD,先将正方形ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A翻折,使得点A落在EF的H上(如图②),折痕交AE于点G,则EG的长度为( )
A. 4![]() ﹣6 B. 2
﹣6 B. 2![]() ﹣3 C. 8﹣4
﹣3 C. 8﹣4![]() D. 4﹣2
D. 4﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
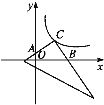
【题目】一直角三角形放置在如图所示的平面直角坐标系中,直角顶点C刚好落在反比例函数y=![]() 的图象的一支上,两直角边分别交y、x轴于A、B两点.当CA=CB时,四边形CAOB的面积为( )
的图象的一支上,两直角边分别交y、x轴于A、B两点.当CA=CB时,四边形CAOB的面积为( )
A. 4 B. 8 C. 2![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
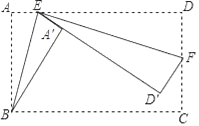
【题目】如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2﹣6x+c的图象过A(﹣1,y1),B(2,y2),C(3,y3),则y1、y2、y3的大小关系是( )
A. y1>y2>y3 B. y1>y3>y2 C. y2>y1>y3 D. y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
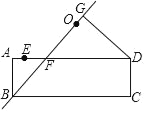
【题目】如图,矩形ABCD中,AB=3,AD=9,点E在边AD上,AE=1,过E、D两点的圆的圆心O在边AD的上方,直线BO交AD于点F,作DG⊥BO,垂足为G.当△ABF与△DFG全等时,⊙O的半径为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,
(1)求等边三角形的高;
(2)求CE的长度;
(3)若将等边三角形ABC绕点C顺时针旋转,旋转角为α(0°<α<360°),求α为多少时,等边三角形的边所在的直线与圆相切.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com