
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,
(1)如图1,若AB∥ON,则
①∠ABO的度数是______;
②当∠BAD=∠ABD时,x=______;
当∠BAD=∠BDA时,x=______;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.

【答案】(1)①18°;②126°;③63°;(2)当x=18、36、54时,△ADB中有两个相等的角.
【解析】
(1)运用平行线的性质以及角平分线的定义,可得∠ABO的度数;根据∠ABO、∠BAD的度数以及△AOB的内角和,可得x的值;
(2)根据三角形内角和定理以及直角的度数,可得x的值.
解:(1)如图1,①∵∠MON=36°,OE平分∠MON,
∴∠AOB=∠BON=18°,
∵AB∥ON,
∴∠ABO=18°;
②当∠BAD=∠ABD时,∠BAD=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°-18°×3=126°;
③当∠BAD=∠BDA时,∵∠ABO=18°,
∴∠BAD=81°,∠AOB=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°-18°-18°-81°=63°,
故答案为①18°;②126°;③63°;
(2)如图2,存在这样的x的值,使得△ADB中有两个相等的角.
∵AB⊥OM,∠MON=36°,OE平分∠MON,
∴∠AOB=18°,∠ABO=72°,
若∠BAD=∠ABD=72°,则∠OAC=90°-72°=18°;
若∠BAD=∠BDA=(180°-72°)÷2=54°,则∠OAC=90°-54°=36°;
若∠ADB=∠ABD=72°,则∠BAD=36°,故∠OAC=90°-36°=54°;
综上所述,当x=18、36、54时,△ADB中有两个相等的角.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】元宵节将至,我校组织学生制作并选送50盏花灯,共包括传统花灯、创意花灯和现代花灯三大种.已知每盏传统花灯需要35元材料费,每盏创意花灯需要33元材料费,每盏现代花灯需要30元材料费.
(1)如果我校选送20盏现代花灯,已知传统花灯数量不少于5盏且总材料费不得超过1605元,请问选送传统花灯、创意花灯的数量有哪几种方案?
(2)当三种花灯材料总费用为1535元时,求选送传统花灯、创意花灯、现代花灯各几盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角△ABC中,AB=AC,∠BAC=90°,过点B,点C分别作经过点A的直线l的垂线,垂足分别为M、N.
(1)请找到一对全等三角形,并说明理由;
(2)BM,CN,MN之间有何数量关系?并说明理由;
(3)若BM=3,CN=5,求四边形MNCB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区果农收获草莓30吨,枇杷13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往省城,已知甲种货车可装草莓4吨和枇杷1吨,乙种货车可装草莓、枇杷各2吨.
(1)该果农安排甲、乙两种货车时有几种方案请您帮助设计出来;
(2)若甲种货车每辆要付运输费2 000元,乙种货车每辆要付运输费1 300元,则该果农应选择哪种运输方案才能使运费最少,最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )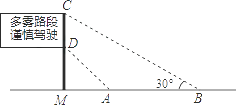
A.4 ![]() 米
米
B.(2 ![]() +2)米
+2)米
C.(4 ![]() ﹣4)米
﹣4)米
D.(4 ![]() ﹣4)米
﹣4)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校“阳光体育”活动的开展情况,从该校1000名学生中随机抽取部分学生进行问卷调查(每名学生只能填写一项自己最喜欢的体育项目),并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中信息,解答下列问题:
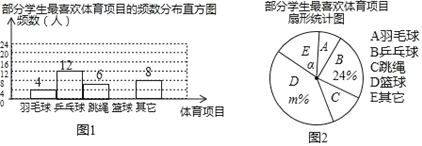
(1)被调查的学生共有多少人?
(2)扇形统计图中m的值和a的度数分别是多少?
(3)根据部分学生最喜欢体育项目的调查情况,请估计全校学生中最喜欢篮球的人数大约有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com