
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 图像上的任意一点,过点
图像上的任意一点,过点![]() 作
作![]() ∥
∥![]() 轴,交另一个反比例函数
轴,交另一个反比例函数![]() 的图像于点
的图像于点![]() .
.
(1)若![]() ,则
,则![]() ______ ;
______ ;
(2)当![]() 时, 若点
时, 若点![]() 的横坐标是1,求
的横坐标是1,求![]() 的度数;
的度数;
(3)如图,若不论点![]() 在何处,反比例函数
在何处,反比例函数![]() 图像上总存在一点
图像上总存在一点![]() ,使得四边形
,使得四边形![]() 为平行四边形,求
为平行四边形,求![]() 的值.
的值.

【答案】(1)k=-4;(2)∠AOB=90°;(3)k=-4.
【解析】(1)AB交y轴于H,根据反比例函数的比例系数的几何意义得S△AOH=![]() ×2=1,S△BOH=
×2=1,S△BOH=![]() |k|,由于S△AOB=3,则1+
|k|,由于S△AOB=3,则1+![]() |k|=3,解得k=4或-4,由于k<0,所以k=-4;
|k|=3,解得k=4或-4,由于k<0,所以k=-4;
(2)①先确定A点坐标为(1,2),B点坐标为(-4,2),根据勾股定理计算出OA=![]() ,由于
,由于![]() =
=![]() ,∠HAO=∠OAB,根据相似三角形的判定得到△HAO∽△OAB,所以∠AOB=∠OHA=90°,
,∠HAO=∠OAB,根据相似三角形的判定得到△HAO∽△OAB,所以∠AOB=∠OHA=90°,
(3)作AE⊥x轴于点E,作DF⊥AB于点F,连接BD,证△DBF≌△AOE,得出D点的坐标即可得出![]() 的值.
的值.
解:(1)连结OD交AB于P,如图1,

设A点坐标为(t, ![]() ),则B点坐标为(
),则B点坐标为(![]() ,
, ![]() ),
),
根据平行四边形的性质得PA=PB,PD=PO,根据线段中点坐标公式得到P点坐标为(![]() ,
, ![]() ),则D点坐标为(
),则D点坐标为(![]() ,
, ![]() ),然后把D(
),然后把D(![]() ,
, ![]() )代入y=
)代入y=![]() 得
得![]()
![]() =k,于是可解得k=-4.
=k,于是可解得k=-4.
(2)由题意,得:A(1,2)B(-4,2)
设AB交y轴于点E,则AE=1,OE=2,EB=4,∴AB=5.
∵OA2 =AE2+OE2=12+22=5,OB2=OE2+BE2=22+42=20,
∴OA2+OB2=5+20=25=AB2.
∴△AOB为直角三角形,且∠AOB=90°.
(3)存在点D在点B上方。设A(a,b),B(m,b),
作AE⊥x轴于点E,作DF⊥AB于点F,连接BD. 则:AE=b,OE=a,
∵四边形AOBD是平行四边形,
∴BD=AO,BD//AO,
∴△DBF≌△AOE,
∴BF=OE=a,DF=AE=b ,
∴D(m+a,b+b),即:D(m+a,2b) .
∵2b(m+a)=k,即:2bm+2ba=k且ba=2,bm=k,
∴2k+4=k ,即:k=-4 .
“点睛”本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、反比例函数的比例系数的几何意义和平行四边形的性质;会利用相似比进行计算.


科目:初中数学 来源: 题型:
【题目】方程(x﹣3)2=m2的解是( )
A. x1=m,x2=﹣m B. x1=3+m,x2=3﹣m
C. x1=3+m,x2=﹣3﹣m D. x1=3+m,x2=﹣3+m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴p=![]() =6
=6
∴S=![]() =
=![]() =6
=6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
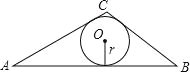
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A (16,0)、C (0,8),四边形OABC是矩形,D、E分别是OA、BC边上的点,沿着DE折叠矩形,点A恰好落往y轴上的点C处,点B落在点B'处。
(1) 求D、E两点的坐标;
(2) 反比例函数y =![]() (k >0) 在第一象限的图像经过E点,判断B′是否在这个反比例函数的图像上? 并说明理由;
(k >0) 在第一象限的图像经过E点,判断B′是否在这个反比例函数的图像上? 并说明理由;
(3) 点F是 (2) 中反比例函数的图像与原矩形的AB边的交点,点G在平面直角坐标系中,以点D、E、F、G为顶点的四边形是平行四边形,求G点的坐标.(直接写出答案)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com