
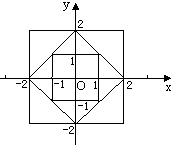
如图所示,第一个正方形的四个顶点分别为(1,1),(-1,1),(-1,-1),(1,-1);第二个正方形的四个顶点分别是(2,0),(0,2),(-2,0),(0,-2);第三个正方形的顶点分别是(2,2),(-2,2),(-2,-2),(2,-2).按此规律,第四个正方形的四个顶点坐标是什么?它的面积是多少?
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•黄石)如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=
(2012•黄石)如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 △ABC是顶点在如图所示的方格纸中的格点上的三角形.
△ABC是顶点在如图所示的方格纸中的格点上的三角形.查看答案和解析>>
科目:初中数学 来源:2006年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
如图①,正方形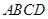 的顶点
的顶点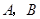 的坐标分别为
的坐标分别为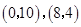 ,顶点
,顶点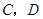 在第一象限.点
在第一象限.点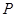 从点
从点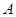 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点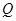 从点
从点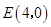 出发,沿
出发,沿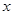 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点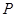 到达点
到达点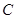 时,
时,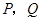 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为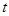 秒.
秒.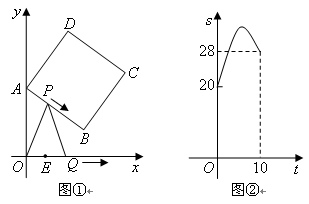
(1)求正方形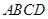 的边长.(2分)
的边长.(2分)
(2)当点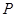 在
在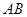 边上运动时,
边上运动时,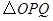 的面积
的面积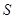 (平方单位)与时间
(平方单位)与时间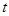 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求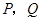 两点的运动速度.(2分)
两点的运动速度.(2分)
(3)求(2)中面积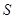 (平方单位)与时间
(平方单位)与时间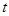 (秒)的函数关系式及面积
(秒)的函数关系式及面积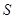 取最大值时点
取最大值时点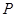 的坐标.(4分)
的坐标.(4分)
(4)若点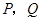 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点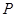 沿着
沿着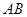 边运动时,
边运动时,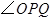 的大小随着时间
的大小随着时间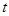 的增大而增大;沿着
的增大而增大;沿着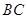 边运动时,
边运动时,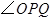 的大小随着时间
的大小随着时间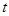 的增大而减小.当点
的增大而减小.当点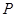 沿着这两边运动时,使
沿着这两边运动时,使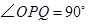 的点
的点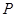 有 个.(2分)
有 个.(2分)
(抛物线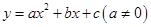 的顶点坐标是
的顶点坐标是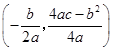 .)
.)
查看答案和解析>>
科目:初中数学 来源:2006年初中毕业升学考试(吉林长春卷)数学(解析版) 题型:解答题
如图①,正方形 的顶点
的顶点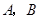 的坐标分别为
的坐标分别为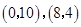 ,顶点
,顶点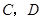 在第一象限.点
在第一象限.点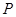 从点
从点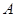 出发,沿正方形按逆时针方向匀速运动,同时,点
出发,沿正方形按逆时针方向匀速运动,同时,点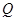 从点
从点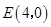 出发,沿
出发,沿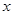 轴正方向以相同速度运动.当点
轴正方向以相同速度运动.当点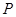 到达点
到达点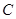 时,
时,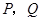 两点同时停止运动,设运动的时间为
两点同时停止运动,设运动的时间为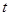 秒.
秒.

(1)求正方形 的边长.(2分)
的边长.(2分)
(2)当点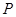 在
在 边上运动时,
边上运动时,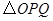 的面积
的面积 (平方单位)与时间
(平方单位)与时间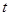 (秒)之间的函数图象为抛物线的一部分(如图②所示),求
(秒)之间的函数图象为抛物线的一部分(如图②所示),求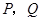 两点的运动速度.(2分)
两点的运动速度.(2分)
(3)求(2)中面积 (平方单位)与时间
(平方单位)与时间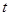 (秒)的函数关系式及面积
(秒)的函数关系式及面积 取最大值时点
取最大值时点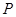 的坐标.(4分)
的坐标.(4分)
(4)若点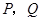 保持(2)中的速度不变,则点
保持(2)中的速度不变,则点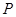 沿着
沿着 边运动时,
边运动时,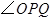 的大小随着时间
的大小随着时间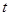 的增大而增大;沿着
的增大而增大;沿着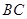 边运动时,
边运动时,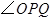 的大小随着时间
的大小随着时间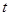 的增大而减小.当点
的增大而减小.当点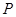 沿着这两边运动时,使
沿着这两边运动时,使 的点
的点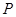 有 个.(2分)
有 个.(2分)
(抛物线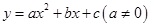 的顶点坐标是
的顶点坐标是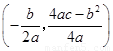 .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com