
分析 首先设甲的速度为x千米/时,则乙的速度为(x-1)千米/时,由题意得等量关系:乙所用时间-甲所用时间=0.5小时,根据等量关系,列出方程,再解即可.
解答 解:设甲的速度为x千米/时,则乙的速度为(x-1)千米/时,由题意得:
$\frac{15}{x-1}$-$\frac{15}{x}$=$\frac{1}{2}$,
解得:x1=6,x2=-5,
经检验:x1=6,x2=-5是原方程的解,但x=-5不合题意,舍去,
x-1=6-1=5,
答:甲的速度为6千米/时,则乙的速度为5千米/时.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,注意不要忘记检验.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在下列解答中,填空或填写适当的理由:
如图,在下列解答中,填空或填写适当的理由:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB为⊙O的直径,弦BD平分∠ABH,过点D作DH⊥BH于点H,BH交⊙O于点C.
如图,已知AB为⊙O的直径,弦BD平分∠ABH,过点D作DH⊥BH于点H,BH交⊙O于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
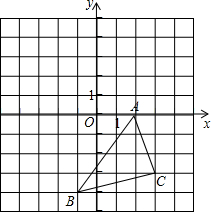 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=15cm,点E在AD上,AE=9cm,连接EC,将矩形ABCD沿BE翻折,点A恰好落在EC上的点A′处,则BC=17cm.
如图,矩形ABCD中,AB=15cm,点E在AD上,AE=9cm,连接EC,将矩形ABCD沿BE翻折,点A恰好落在EC上的点A′处,则BC=17cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com