
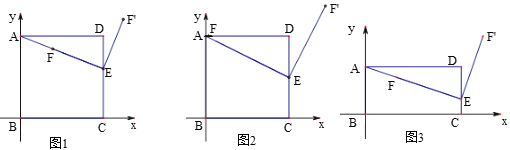
【题目】正方形ABCD的边长为4,以B为原点建立如图1平面直角坐标系中,E是边CD上的一个动点,F是线段AE上一点,将线段EF绕点E顺时针旋转90°得到EF'.
(1)如图2,当E是CD中点,![]() 时,求点F'的坐标.
时,求点F'的坐标.
(2)如图1,若![]() ,且F',D,B在同一直线上时,求DE的长.
,且F',D,B在同一直线上时,求DE的长.
(3)如图3,将正边形ABCD改为矩形,AD=4,AB=2,其他条件不变,若![]() ,且F',D,B在同一直线上时,则DE的长是_______.(请用含n的代数式表示)
,且F',D,B在同一直线上时,则DE的长是_______.(请用含n的代数式表示)
【答案】(1)点F'的坐标是(6,6);(2)![]() ;(3)
;(3)![]()
【解析】
(1)如图2,作EM⊥AB于M,![]() 交CD延长线于H,证明△AME≌△F'HE,求出AM=F'H=2,EM=EH=4,即可解决问题;
交CD延长线于H,证明△AME≌△F'HE,求出AM=F'H=2,EM=EH=4,即可解决问题;
(2)如图1,作FM⊥CD于M,F'H⊥CD交CD延长线于H,连接BF',设DE=x,首先证明FM是三角形的中位线,再利用全等三角形的性质构建方程即可解决问题;
(3)如图3,作FM⊥CD于M,F'H⊥CD交CD延长线于H,连接BF',设DE=x,AE=1,AF=n,利用平行线分线段成比例求出FM,EM,再利用全等三角形的性质求出EH,H F',再根据三角函数求出DH,构建方程即可解决问题.
解:(1)如图2,作EM⊥AB于M,![]() 交CD延长线于H,
交CD延长线于H,
∵E是CD中点,
∴四边形AMED是矩形,
∵∠AME=∠AEF'=∠MEH=∠H=90°,
∴∠AEM+∠AEH=90°,∠AEH+∠HEF'=90°,
∴∠AEM=∠HEF',EA= EF',
∴△AME≌△F'HE,
∴AM=F'H=2,EM=EH=4,
∴F'(6,6);
(2)如图1,作FM⊥CD于M,F'H⊥CD交CD延长线于H,连接BF',设DE=x,
∵![]() ,
,
∴AF=EF,
∵FM∥AD,∴DM=ME=![]() ,FM =
,FM =![]() ,
,
∠AEM+∠HEF'=90°,∠AEM+∠MFE=90°,
∴∠HEF'=∠MFE,
因为∠FME=∠HF'E=90°,EF= EF',
∴△FME≌△EHF',
∴HF'=ME=![]() ,EH=FM=2,
,EH=FM=2,
∵四边形ABCD是正方形,
∴∠HDF'=∠BDC=45°,
∴DH= HF'=![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴DE=![]() .
.
(3)如图3,作FM⊥CD于M,F'H⊥CD交CD延长线于H,连接BF',设DE=x,AE=1,AF=n,
∵FM∥AD,∴![]() ,
,
∴FM=4-4n,EM=x-xn,
由(2)可知△FME≌△EHF',
∴HF'=EM=x-xn,EH=FM=4-4n,
∵![]() ,
,
∴DH=![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.



科目:初中数学 来源: 题型:
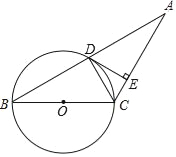
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过点D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接DC,若BC=4,求弧DC与弦DC所围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
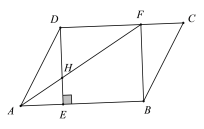
【题目】在平行四边形 ABCD 中,过点 D 作 DE⊥AB 于点 E,点 F 在 CD 上,CF =AE,连接 BF,AF.
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分∠BAD,交DE与H点,且 AB=3AE,BF=6,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
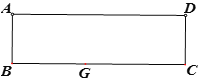
【题目】如图,在矩形纸片ABCD中,AB=4,点G是BC边上一点,且BG=5(BG<CG). 将矩形纸片沿过点G的折痕GE折叠,使点B恰好落在AD边上,折痕与矩形纸片ABCD的边相交于点E,则折痕GE的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
5分以下 | 3 | 0.06 | |
合计 | 50 | 1 |
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
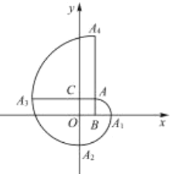
【题目】如图,在平面直角坐标系中,四边形![]() 是正方形,点
是正方形,点![]() 的坐标为
的坐标为![]() ,弧
,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧;弧
为半径的圆弧;弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,弧
为半径的圆弧,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧,弧
为半径的圆弧,弧![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆弧.继续以点
为半径的圆弧.继续以点![]() ,
,![]() ,
,![]() ,
,![]() 为圆心按上述作法得到的曲线
为圆心按上述作法得到的曲线![]() …称为正方形的“渐开线”,则点
…称为正方形的“渐开线”,则点![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
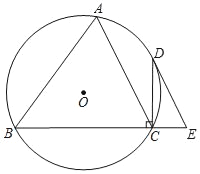
【题目】如图,△ABC内接于⊙O,过点C作BC的垂线交⊙O于D,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com