
| 16 |
| 3 |
| 16 |
| 3 |
| 4n |
| 3n-1 |
| 4n |
| 3n-1 |

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:百分学生作业本课时3练1测 七年级数学(下) 适用人教课标版学生 人教课标版 题型:059
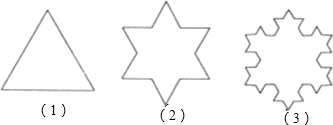
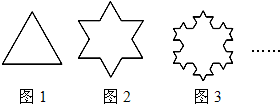
如图,设有一个边长为L的等边三角形,记作A1,如图(1)所示,将A1的每条边三等分,在中间的线段上向图形外作等边三角形,去掉中间线段后所得到的图形记作A2,如图(2)所示,将A2的每条边三等分并重复上述过程,所得到的图形记作A3,如图(3)所示这样,可以得到一系列的图形,请计算图形A1999的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市顺义一中八年级(上)入学数学测试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com