
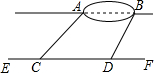
 小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离. 分析 根据题意作出合适的辅助线,画出相应的图形,可以分别求得CM、DN的长,由于AB=CN-CM,从而可以求得AB的长.
解答 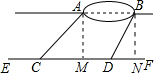 解:作AM⊥EF于点M,作BN⊥EF于点N,如右图所示,
解:作AM⊥EF于点M,作BN⊥EF于点N,如右图所示,
由题意可得,AM=BN=60米,CD=100米,∠ACF=45°,∠BDF=60°,
∴CM=$\frac{AM}{tan45°}=\frac{60}{1}=60$米,
DN=$\frac{BN}{tan60°}=\frac{60}{\sqrt{3}}=20\sqrt{3}$米,
∴AB=CD+DN-CM=100+20$\sqrt{3}$-60=(40+20$\sqrt{3}$)米,
即A、B两点的距离是(40+20$\sqrt{3}$)米.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,画出相应的图形,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:选择题
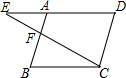 如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )
如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com