
【题目】观察下面三行单项式:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;①
,…;①
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;②
,…;②
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,…;③
,…;③
根据你发现的规律,解答下列问题:
(1)第①行的第8个单项式为 ;
(2)第②行的第9个单项式为 ;
(3)第③行的第n个单项式为 (用含n的式子表示);
(4)取每行的第8个单项式,令这三个单项式的和为A.
当![]() 时,求A的值.
时,求A的值.
【答案】(1)28x8或256x8; (2)(-2)9x9或 -29x9或-512x9; (3)(-1)n(2n +1)xn+1;(4)![]()
【解析】
(1)根据第①行的数字的规律,从第一个单项式开始,后面的单项式系数每次乘以2,指数每次加1,可得第8个单项式;
(2)根据第②行的数字的规律,从第一个单项式开始,后面的单项式系数每次乘以(-2),指数每次加1,可得第9个单项式;
(3)根据第③行的数字规律,结合第②行的数字的规律可知,第n个单项式为(-1)n(2n +1)xn+1;
(4)取每行的第8个单项式,则可得![]() ,把
,把![]() 代入计算即可.
代入计算即可.
解:(1)第①行的第8个单项式为28x8或256x8,
故答案为:28x8或256x8;
(2)第②行的第9个单项式为 (-2)9x9或 -29x9或-512x9 ,
故答案为:(-2)9x9或 -29x9或-512x9;
(3)第③行的第n个单项式为 (-1)n(2n +1)xn+1 ,
故答案为:(-1)n(2n +1)xn+1;
(4) ![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() 、
、![]() ,其中A表示的数为-2,
,其中A表示的数为-2,![]() 表示的数为2,若在数轴上存在一点
表示的数为2,若在数轴上存在一点![]() ,使得
,使得![]() ,则称点
,则称点![]() 叫做点
叫做点![]() 、
、![]() 的“
的“![]() 节点”,例如图1所示,若点
节点”,例如图1所示,若点![]() 表示的数为0,有
表示的数为0,有![]() ,则称点
,则称点![]() 为点
为点![]() 、
、![]() 的“4节点”.
的“4节点”.
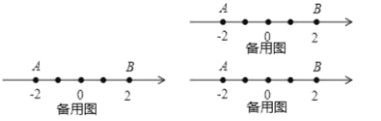
请根据上述规定回答下列问题:
(1)若点![]() 为点
为点![]() 、
、![]() 的“
的“![]() 节点”,且点
节点”,且点![]() 在数轴上表示的数为-4,求
在数轴上表示的数为-4,求![]() 的值.
的值.
(2)若点![]() 是数轴上点
是数轴上点![]() 、
、![]() 的“5节点”,请你直接写出点
的“5节点”,请你直接写出点![]() 表示的数为____________;
表示的数为____________;
(3)若点![]() 在数轴上(不与
在数轴上(不与![]() 、
、![]() 重合),满足
重合),满足![]() 、
、![]() 之间的距离是
之间的距离是![]() 、
、![]() 之间距离的一半,且此时点
之间距离的一半,且此时点![]() 为点
为点![]() 、
、![]() 的“
的“![]() 节点”,求
节点”,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会对多项式(x2+5x+2)(x2+5x+3)﹣12分解因式吗?对结构较复杂的多项式,若把其中某些部分看成一个整体,用新字母代替(即换元),能使复杂的问题简单化、明朗化.从换元的个数看,有一元代换、二元代换等.
对于(x2+5x+2)(x2+5x+3)﹣12.
解法一:设x2+5x=y,
则原式=(y+2)(y+3)﹣12=y2+5y﹣6=(y+6)(y﹣1)
=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).
解法二:设x2+5x+2=y,
则原式=y(y+1)﹣12=y2+y﹣12=(y+4)(y﹣3)
=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).
解法三:设x2+2=m,5x=n,
则原式=(m+n)(m+n+1)﹣12=(m+n)2+(m+n)﹣12=(m+n+4)(m+n﹣3)
=(x2+5x+6)(x2+5x﹣1)=(x+2)(x+3)(x2+5x﹣1).
按照上面介绍的方法对下列多项式分解因式:
(1)(x2+x﹣4)(x2+x+3)+10;
(2)(x+1)(x+2)(x+3)(x+6)+x2;
(3)(x+y﹣2xy)(x+y﹣2)+(xy﹣1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE是以C为公共顶点的两个等腰三角形,且AC=CB,CD=CE,连接BD、AE相交于点M,连接CM,∠CAB=∠CDE=50°,则∠BMC=( )

A. 30°B. 40°C. 50°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
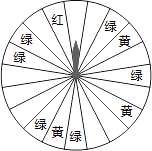
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说
,也就是说![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离,这个结论可以推广为
对应的点之间的距离,这个结论可以推广为![]() 表示数轴上
表示数轴上![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例1:已知![]() ,求
,求![]() 的值.
的值.
解:容易看出,在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例2:已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,求下列各式中的值.
(1)![]()
(2)![]()
(3)由以上探索猜想:对于任何有理数![]() 是否有最小值?如果有,写出最小值;如果没有,请说明理由.
是否有最小值?如果有,写出最小值;如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com