
 如图,AB是⊙O的直径,AC是弦,D是$\widehat{AC}$的中点,DE⊥AB于E,DF交AC于按F,DB交AC于点G.下面结论:①FA=FD=FG;②FG=GC;③CD是DG与DB的比例中项;④$\frac{EO}{OB}$=$\frac{EF}{FD}$,其中正确的结论有3个.
如图,AB是⊙O的直径,AC是弦,D是$\widehat{AC}$的中点,DE⊥AB于E,DF交AC于按F,DB交AC于点G.下面结论:①FA=FD=FG;②FG=GC;③CD是DG与DB的比例中项;④$\frac{EO}{OB}$=$\frac{EF}{FD}$,其中正确的结论有3个. 分析 连接AD,延长DE交⊙O于M,如图1,根据垂径定理得$\widehat{AD}$=$\widehat{AM}$,又由D是$\widehat{AC}$的中点,得到$\widehat{AD}$=$\widehat{AM}$=$\widehat{CD}$,根据圆周角定理得到∠3=∠B,再由AB为直径,得到∠ADB=90°,所以∠3+∠AGD=90°,易得∠1=∠AGD,所以DF=FG;根据圆周角定理由$\widehat{AD}$=$\widehat{AM}$=$\widehat{CD}$,得到∠3=∠2,于是得到FA=FD=FG;根据圆周角定理,由AB为直径得到∠ADB=∠ACB=90°,然后证明∠FGD=∠FDG,得到FD=FG,加上FA=FD,所以FA=FG,接着在△ADF和△CDG中,∠DAF=∠DCG,DA=DC,假设CG=FG,则AF=CG,则可判断△ADF≌△CDG,而△ADF为等腰三角形,所以△DCG也为等腰三角形,于是得到∠DCA=∠CDB,所以点C为BD弧的中点,即C、D为半圆的三等分点,这与题设不符,所以CG与FG不能确定相等;通过△CDG∽△BCD,根据相似三角形的性质得到CD是DG与DB的比例中项;如图2,连接OD,则OD⊥AC,通过△AEF∽△ODE,根据相似三角形的性质得到$\frac{AF}{OD}=\frac{EF}{OE}$,等量代换即可得到结论.
解答 证明:如图1,连接AD,延长DE交⊙O于M,如图1,
∵DE⊥AB,
∴$\widehat{AD}$=$\widehat{AM}$,
∵D是$\widehat{AC}$的中点,
∴$\widehat{AD}$=$\widehat{AM}$=$\widehat{CD}$,
∴∠3=∠B,
∵AB为直径,
∴∠ADB=90°,
∴∠3+∠AGD=90°,
∵∠B+∠1=90°,
∴∠1=∠AGD,
∴DF=FG;
∵$\widehat{AD}$=$\widehat{AM}$=$\widehat{CD}$,
∴∠3=∠2,
∴AF=FG,
∴FA=FD=FG;故①正确;
如图1,连接BC,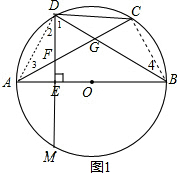 ∵AB为直径,
∵AB为直径,
∴∠ADB=∠ACB=90°,
∴∠FDG+∠ADQ=90°,∠CGB+∠4=90°,
∵∠CGB=∠FGD,∠4=∠ADQ,
∴∠FGD=∠FDG,
∴FD=FG,
∵FA=FD,
∴FA=FG,
在△ADF和△CDG中,
∠DAF=∠DCG,DA=DC,
若CG=FG,则AF=CG,则可判断△ADF≌△CDG,
∵△ADF为等腰三角形,
∴△DCG也为等腰三角形,
∴∠DCA=∠CDB,
∴点C为BD弧的中点,即C、D为半圆的三等分点,这与题设不符,
∴CG与FG不能确定相等,故②错误;
∵∠DCA=∠4,∠CDG=∠CDG,
∴△CDG∽△BCD,
∴$\frac{DG}{CD}=\frac{CD}{BD}$,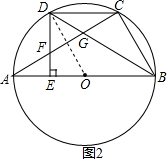
∴CD2=DG•BD,
∴CD是DG与DB的比例中项,故③正确;
如图2,连接OD,则OD⊥AC,
∴∠A=∠EDO,
∵∠AEF=∠DEO=90°,
∴△AEF∽△ODE,
∴$\frac{AF}{OD}=\frac{EF}{OE}$,
∵AF=DF,OD=OB,
∴$\frac{EO}{OB}$=$\frac{EF}{FD}$,故④正确.
故答案为:3.
点评 本题考查了相似三角形的判定和性质,圆周角定理,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2 | B. | $\frac{1}{2}$a2 | C. | $\frac{1}{4}$a2 | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论,其中正确的是( )| A. | a>0 | B. | b<0 | C. | c<0 | D. | a-b+c<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com