
科目:初中数学 来源: 题型:
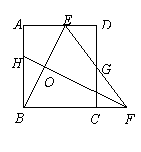
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,B E的垂直平分线交BC的延长线于点F,连结EF交CD于点G,若G是CD的中点,则BC的长是 .
E的垂直平分线交BC的延长线于点F,连结EF交CD于点G,若G是CD的中点,则BC的长是 .
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )

|
| A. | AB=DE | B. | ∠B=∠E | C. | EF=BC | D. | EF∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
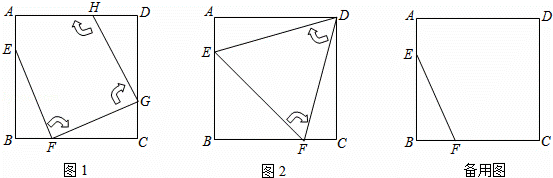
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B,C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依次操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 等边三角形 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 正方形 ,此时AE与BF的数量关系是 AE=BF ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围;
(3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
小军家距学校5千米,原来他骑自行车上学,学校为保障学生安全,新购进校车接送学生,若小车速度是他骑车速度的2倍,现在小军乘小车上学可以从家晚10分钟出发,结果与原来到校时间相同.设小军骑车的速度为x千米/小时,则所列方程正确的为( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
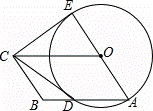
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,AC=BC= ,将Rt△ABC绕A点按逆时针方向旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则途中阴影部分的面积是( )
,将Rt△ABC绕A点按逆时针方向旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则途中阴影部分的面积是( )
A. B.
B.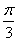 C.
C. D.
D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com